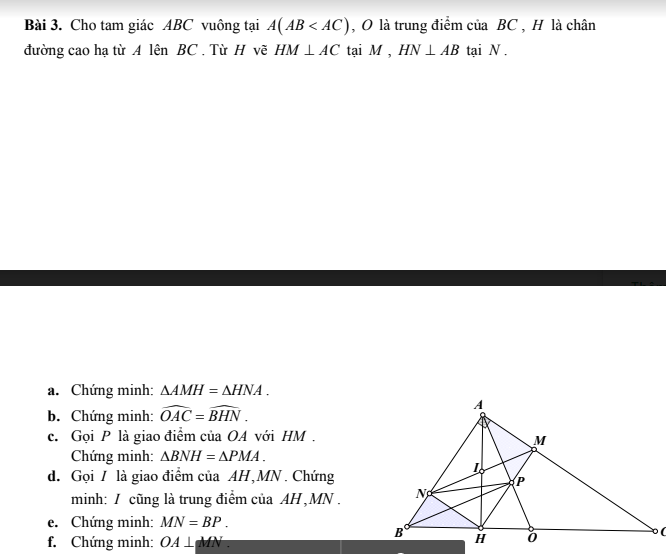
a)Xét tam giác AMH và tam giác HNA có
ANH=AMH=90\(^0\)(gt)
AH chung
NAH=AHM(slt)
=> tam giác AMH=HNA(g.c.g)
b)T có NH//AC(cùng vuông góc HM)
=>BHN=HCA(đồng vị)
Hay BHN=OCA
Mak OCA=OAC(do AO là đường trung tuyến =>AO=OC=OB=\(\dfrac{BC}{2}\)=>Tam giác AOC cân)
=> BHN=OAC
C)Tcos HNA=HMA=NAM=90\(^0\)
=> AMHN là hình chữ nhật=>HN=AM
Xét tam giác BNH và tam giác PMA có
HN=AM(Cmt)
PAM=BNH=90\(^0\)
BHN=PAM
=>tam giác BNH= tam giác PMA(g.c.g)
d)T có ANHM là Hình chữ nhật (Cmt) đồng thời là HÌnh bình hành
Mak I là giao của AH và MN
=> I là trung điểm của AH và MN
e)Taco BN//PM( cùng vuông góc với AC)
Mak BN=PM(do tam giác BNH= tam giác AMP)
=> BNPM là Hình bình Hành
=> MN=BP
f)Taco BH+HO=BO
AP+PO=AO
Mak AO=BO(tính chất đường trung tuyến trong tam giác vuông)
BH=AP ( tam giác BNH= tam giác PAM)
=> HO=PO
Xét tam giác BOP và tam giác HOA có
BOA chung
BO=AO(cmt)
HO=OP(cmt)
=> tam giác BOP= tam giác HOA(c.g.c)
=>AHO=BPO=90\(^0\)
=> BP\(\perp\)AO
mak BP//MN(cmt)
=> AO\(\perp\)MN(đpcm)
















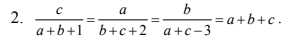 tìm a, b, c
tìm a, b, c