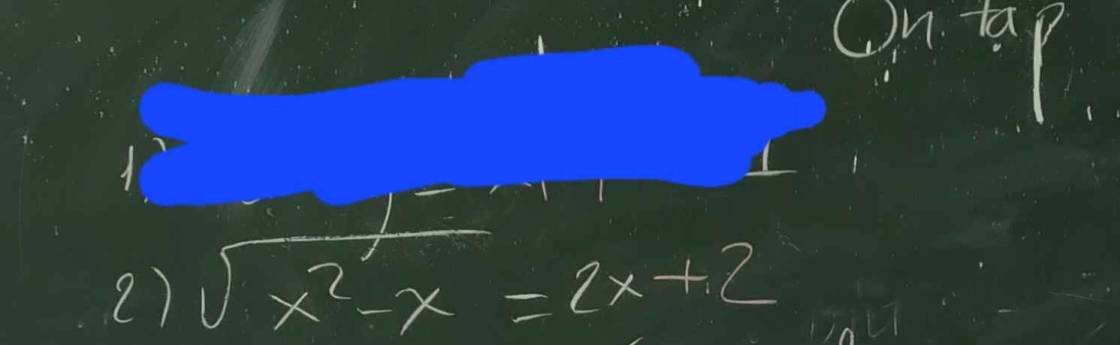\(\sqrt{x^2-x}=2x+2\)
Bình phương 2 vế của pt, ta được :
\(x^2-x=\left(2x+2\right)^2\)
\(\Rightarrow x^2-x=4x^2+8x+4\)
\(\Rightarrow x^2-4x^2-x-8x-4=0\)
\(\Rightarrow-3x^2-9x-4=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{-9+\sqrt{33}}{6}\\x=\dfrac{-9-\sqrt{33}}{6}\end{matrix}\right.\)
Thay lần lượt các giá trị trên vào pt, ta thấy không có giá trị nào thỏa
Vậy pt vô nghiệm.
Đúng 1
Bình luận (0)
