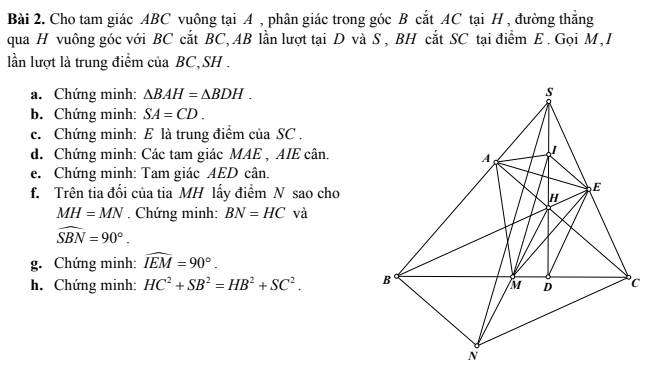
a) Xét tam giác ABM và tam giác CDM có:
+ BM = DM (M là trung điểm BD).
+ ^AMB = ^CMD (đối đỉnh).
+ AM = CM (M là trung điểm AC).
=> Tam giác ABM = Tam giác CDM (c - g - c).
b) Vì tam giác ABM = tam giác CDM (cmt).
=> AB = CD (2 cạnh tương ứng).
Ta có: ^BAM = 90o (Tam giác ABC vuông tại A).
Mà ^BAM = ^DCM (tam giác ABM = tam giác CDM).
=> ^BAM = ^DCM = 90o.
=> CD vuông góc AC (đpcm).
c) Ta có: AB = CD (cmt).
Mà CD = CE (gt).
Xét tứ giác ACEB có:
+ AB = CE (cmt).
+ AB // AC (do cùng vuông óc với AC).
=> Tứ giác ADEB là hình bình hành (dhnb).
=> Giao điểm của 2 đường chéo BC và AE là trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của BC (gt).
=> O là trung điểm của AE.
=> 3 điểm A; O; E thẳng hàng (đpcm).