a, Hoành độ giao điểm là nghiệm của pt :
\(x^2=3x+m-4\\ \Rightarrow x^2-3x-m+4=0\\\Delta=\left(-3\right)^2-4.1.\left(4-m\right)\\ =9-16+4m\\ =4m-7\)
phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Rightarrow4m-7>0\\ \Rightarrow m>\dfrac{7}{4}\)
b, Áp dụng hệ thức vi ét : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1.x_2=4-m\end{matrix}\right.\)
\(x_1^2-x^2_2=3\\ \Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=3\\ \Leftrightarrow\left(4-m\right).3=3\\ \Leftrightarrow12-3m=3\\ \Leftrightarrow3m=12-3\\ \Leftrightarrow3m=9\\ \Leftrightarrow m=9\left(t/mđk\right)\)
:)) câu b mình nhầm xíu nhe
b, Áp dụng hệ thức vi ét : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=3\left(1\right)\\x_1x_2=\dfrac{c}{a}=4-m\left(3\right)\end{matrix}\right.\)
\(x_1^2-x_2^2=3\\ \Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=3\\ \Leftrightarrow\left(x_1-x_2\right).3=3\\ \Leftrightarrow x_1-x_2=1\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) ta có hpt :
\(\left\{{}\begin{matrix}x_1+x_2=3\\x_1-x_2=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=1\end{matrix}\right.\)
Thay \(x_1=2;x_2=1\) vào \(\left(3\right)\)
\(\Rightarrow2.1=4-m\\ \Leftrightarrow4-m=2\\ \Leftrightarrow m=2\left(t/mđk\right)\)

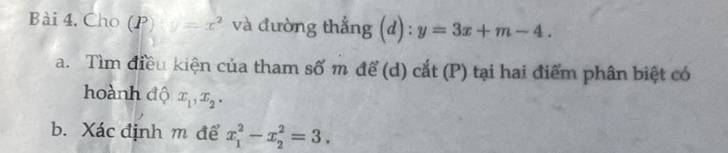









 giúp mình câu b với ạ
giúp mình câu b với ạ

