\(1,A=\dfrac{2\cdot6}{6+3}=\dfrac{12}{9}=\dfrac{4}{3}\\ 2,P=A+B=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\\ 3,P< 2\Leftrightarrow\dfrac{6\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}=\dfrac{5\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\\ \Leftrightarrow\sqrt{x}-3< 0\left(5\sqrt{x}+3>0;2>0\right)\\ \Leftrightarrow x< 9\Leftrightarrow0\le x< 9\)
Đúng 0
Bình luận (4)
Các câu hỏi tương tự

làm giúp mình câu 5 :câu 3 với!giải dõ hộ mình với ạ!
Giúp mình 3 câu này vs ạ cần gấp ạ 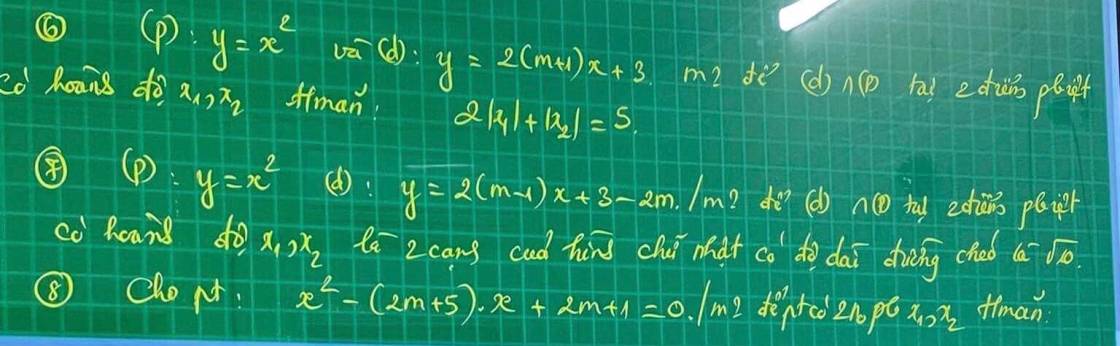
 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
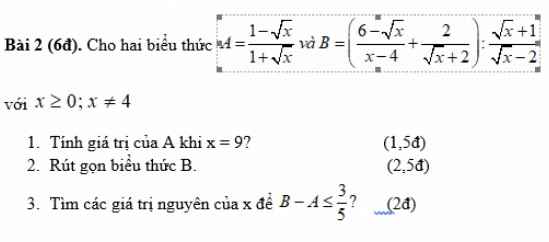 giúp mình câu 3 ạ
giúp mình câu 3 ạ
Ai giúp mình câu 3 với,mình cảm ơn ạ
Ai giúp mình làm 3 câu này với ạ mình đang cần gấp. Cảm ơn mn nhiều ạ.
làm giúp mình câu 3 ạ![]()

giúp mình câu 3 với ạ :( 
 giúp mình câu 3 vs ạ.
giúp mình câu 3 vs ạ.

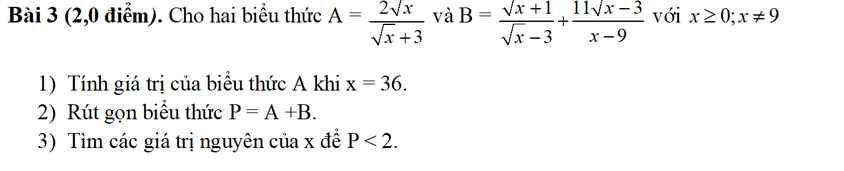 giúp mình câu 3 ạ
giúp mình câu 3 ạ









