Các câu hỏi tương tự
Cho hình chóp S.ABC có ABC là tam giác vuông tại A và SB vuông góc với mặt phẳng (ABC).Gọi BH là đường cao của tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳngđịnh sai?A. SA ⊥ BC. B. BH ⊥ SC. C. SA ⊥ AC. D. BH ⊥ AC.help me !!!
Đọc tiếp
Cho hình chóp S.ABC có ABC là tam giác vuông tại A và SB vuông góc với mặt phẳng (ABC).
Gọi BH là đường cao của tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng
định sai?
A. SA ⊥ BC. B. BH ⊥ SC. C. SA ⊥ AC. D. BH ⊥ AC.
help me !!!
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA
(ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
1) Chứng minh tam giác SBC vuông .
2) Chứng minh tam giác AHK vuông và tính diện tích tam giác AHK .
3) Tính góc giữa AK và (SBC) .
Cho chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB a, SA 5a. Gọi D, E là hình chiếu của A trên SB, SC. Thể tích khối chóp A.BCED là
A
.
85
a
3
1352
B
.
22
a
3
289
C...
Đọc tiếp
Cho chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB = a, SA = 5a. Gọi D, E là hình chiếu của A trên SB, SC. Thể tích khối chóp A.BCED là
A . 85 a 3 1352
B . 22 a 3 289
C . 19 a 3 200
D . 3 a 3 25
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB a
10
, BC 2a, SC 2a
3
. Thể tích khối chóp S.ABC là:
A
.
3
a
3
2
B
.
3
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB = a 10 , BC = 2a, SC = 2a 3 . Thể tích khối chóp S.ABC là:
A . 3 a 3 2
B . 3 a 3 2
C . 3 a 3
D . a 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết Tính thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết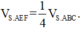 
Tính thể tích V của khối chóp S.ABC
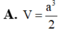
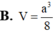
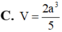
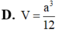
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,ABa,SAperp AB,SCperp BC,SB2a.Gọi M,N lần lượt là trung điểm SA,BC. Gọi alpha là góc giữa MN với left(ABCright) .Tính cosalpha.
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB=a,SA\perp AB,SC\perp BC,SB=2a.\)Gọi \(M,N\) lần lượt là trung điểm \(SA,BC\). Gọi \(\alpha\) là góc giữa \(MN\) với \(\left(ABC\right)\) .Tính \(cos\alpha\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông (ABC) SA= a cân 3; AB=a
A: Chứng minh (SAB) vuông (SAC)
B: Gọi M là trung điểm của BC, chứng minh BC vuông góc vs SM
C: Tính góc giữa SC và (ABC
Bài 9 : Cho hình chóp S.ABC có đáy là tam giác đều tại A, SA vuông góc với (ABC), SB = 5a. Gọi I là trung điểm của BC. Tính góc giữa cánh SI và mặt dáy là
Cho hình chóp S.ABC có đấy ABC là tam giác đều cạnh a, SA = SB = SC = 2a. Gọi o là trung điểm AC, G là trọng tâm tam giác ABC a) chứng minh (SGO) vuông góc với (ABC) b) tính góc giữa hai mặt phẳng (SAB) và (ABC) c) tính khoảng cách giữa AB và SC
Cho hình chóp S.ABC có ABC là tam giác vuông tại B, AB a, BC 2a. Biết
S
A
⊥
A
B
,
S
C
⊥
B
C
, góc giữa SC và (ABC) bằng
60
0
. Độ dài cạnh SB bằng: A.
2
a
B.
2
2
a...
Đọc tiếp
Cho hình chóp S.ABC có ABC là tam giác vuông tại B, AB = a, BC = 2a. Biết S A ⊥ A B , S C ⊥ B C , góc giữa SC và (ABC) bằng 60 0 . Độ dài cạnh SB bằng:
A. 2 a
B. 2 2 a
C. 3 a
D. 3 2 a