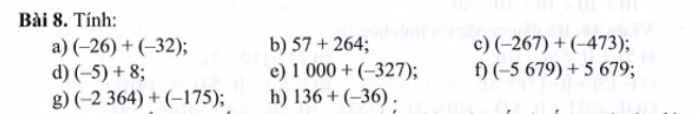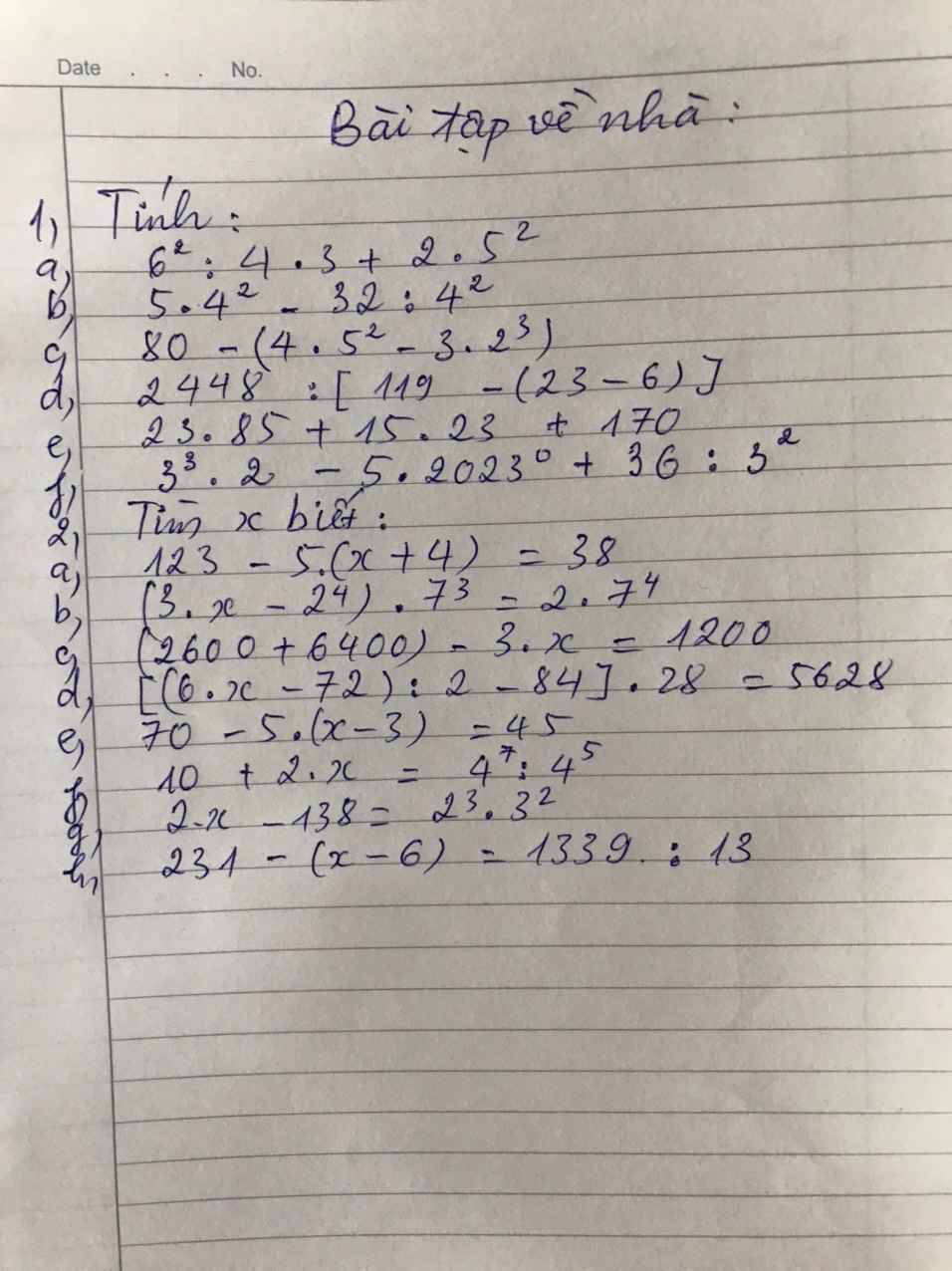Câu 1:
a) \(2^3+3.\left(\dfrac{1}{3}\right)^0-2^{-2}.4+\left[\left(-2\right)^3:\dfrac{1}{2}\right].8\)
\(=8+3-1-16.8\)
\(=10-128\)
\(=-118\)
b) \(\dfrac{-19}{2^3.3^2.5}+\left(-3\dfrac{1}{2}\right)^2:1,2-\left(-1\dfrac{1}{3}\right)^3:\dfrac{5}{6}\)
\(=\dfrac{-19}{360}+\left(-\dfrac{7}{2}\right)^2:1,2-\left(-\dfrac{4}{3}\right)^3:\dfrac{5}{6}\)
\(=-\dfrac{19}{360}+\dfrac{49}{4}:\dfrac{6}{5}-\left(\dfrac{-64}{27}\right):\dfrac{5}{6}\)
\(=-\dfrac{19}{360}+\dfrac{245}{24}+\dfrac{128}{45}\)
\(=-\dfrac{19}{360}+\dfrac{3675}{360}+\dfrac{1024}{360}\)
\(=\dfrac{4680}{360}\)
\(=13\)
c) \(\dfrac{10^3+5.10^2.5^3}{6^3+3.6^2+3^3}\)
\(=\dfrac{2^3.5^3+5.2^2.5^2.5^3}{2^3.3^3+3.2^2.3^2+3^3}\)
\(=\dfrac{5^3.2^2.\left(2+5^3\right)}{3^3.\left(2^3+2^2+1\right)}\)
\(=\dfrac{500.129}{27.13}\)
\(=\dfrac{21500}{117}\)
Câu 2:
a) \(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Do \(9>8\Rightarrow9^{100}>8^{100}\)
Vậy \(3^{200}>2^{300}\)
b) \(9^{12}=\left(9^3\right)^4=729^4\)
\(26^8=\left(26^2\right)^4=676^4\)
Do \(729>676\Rightarrow729^4>626^4\)
Vậy \(9^{12}>26^8\)
Câu 3.
a) \(\left(2x-3\right)^2=25\)
\(\Rightarrow2x-3=5\) hoặc \(2x-3=-5\)
*) \(2x-3=5\)
\(2x=8\)
\(x=4\)
*) \(2x-3=-5\)
\(2x=-2\)
\(x=-1\)
Vậy \(x=-1;x=4\)
b) \(\dfrac{27}{3^x}=3\)
\(27=3.3^x\)
\(3^{x+1}=27\)
\(x+1=3\)
\(x=2\)
Vậy \(x=2\)
c) \(\left(\dfrac{8}{3}-2x\right)^4=625\)
\(\Rightarrow\dfrac{8}{3}-2x=5\) hoặc \(\dfrac{8}{3}-2x=-5\)
*) \(\dfrac{8}{3}-2x=5\)
\(2x=-\dfrac{7}{3}\)
\(x=\dfrac{-7}{6}\)
*) \(\dfrac{8}{3}-2x=-5\)
\(2x=\dfrac{23}{3}\)
\(x=\dfrac{23}{6}\)
Vậy \(x=-\dfrac{7}{6};x=\dfrac{23}{6}\)
d) \(x^3=0,125\)
\(x^3=\left(0,5\right)^3\)
\(x=0,5\)
Vậy \(x=0,5\)
\(a,\left(2x-3\right)^2=25.\\ \Leftrightarrow\left[{}\begin{matrix}\left(2x-3\right)^2=5^2.\\\left(2x-3\right)^2=\left(-5\right)^2.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=5.\\2x-3=-5.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4.\\x=-1.\end{matrix}\right.\)
\(b,\dfrac{27}{3^x}=3.\\ \Leftrightarrow3^x=9.\\ \Leftrightarrow3^x=3^2.\\ \Rightarrow x=2.\)
\(c,\left(\dfrac{8}{3}-2x\right)^4=625.\\ \Leftrightarrow\left[{}\begin{matrix}\left(\dfrac{8}{3}-2x\right)^4=5^4.\\\left(\dfrac{8}{3}-2x\right)^4=\left(-5\right)^4.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{8}{3}-2x=5.\\\dfrac{8}{3}-2x=-5.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{6}.\\x=\dfrac{23}{6}.\end{matrix}\right.\)
\(d,x^3=0,125.\\ \Leftrightarrow x^3=0,5^3.\\ \Rightarrow x=0,5.\)