\(a,b,c>0\)
\(\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^3+b^3+c^3}{2abc}\)
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^3}{2abc}+\dfrac{b^3}{2abc}+\dfrac{c^3}{2abc}\)
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}\) (*)
-Áp dụng BĐT AM-GM (trung bình cộng-trung bình nhân) cho 2 số dương, ta có:
\(\left\{{}\begin{matrix}b^2+c^2\ge2bc\\c^2+a^2\ge2ca\\a^2+b^2\ge2ab\end{matrix}\right.\)
-Do đó: \(\left\{{}\begin{matrix}\dfrac{a^2}{b^2+c^2}\le\dfrac{a^2}{2bc}\\\dfrac{b^2}{c^2+a^2}\le\dfrac{b^2}{2ca}\\\dfrac{c^2}{a^2+b^2}\le\dfrac{c^2}{2ab}\end{matrix}\right.\)
-Cộng các vế của các BĐT, ta có:
\(\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}\)
\(\Rightarrow\) (*) đúng
-Vậy BĐT đã được c/m.
-Dấu "=" xảy ra khi \(a=b=c\)








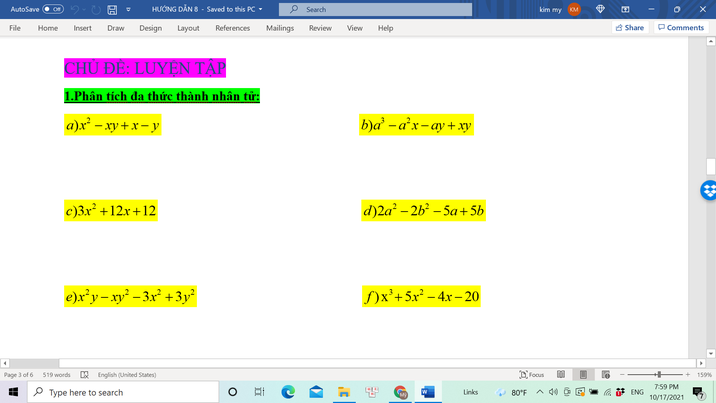




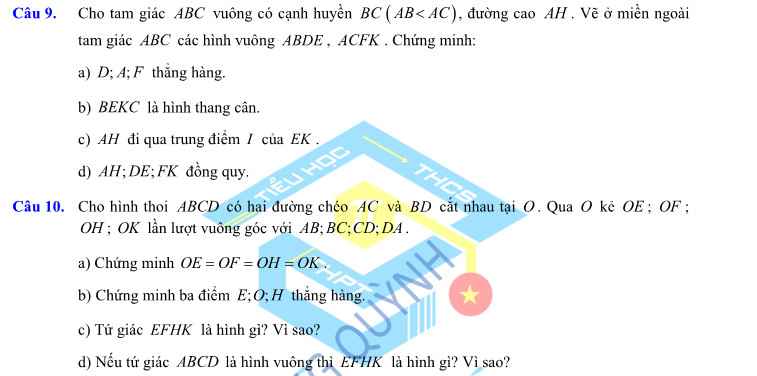


 AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ
AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ