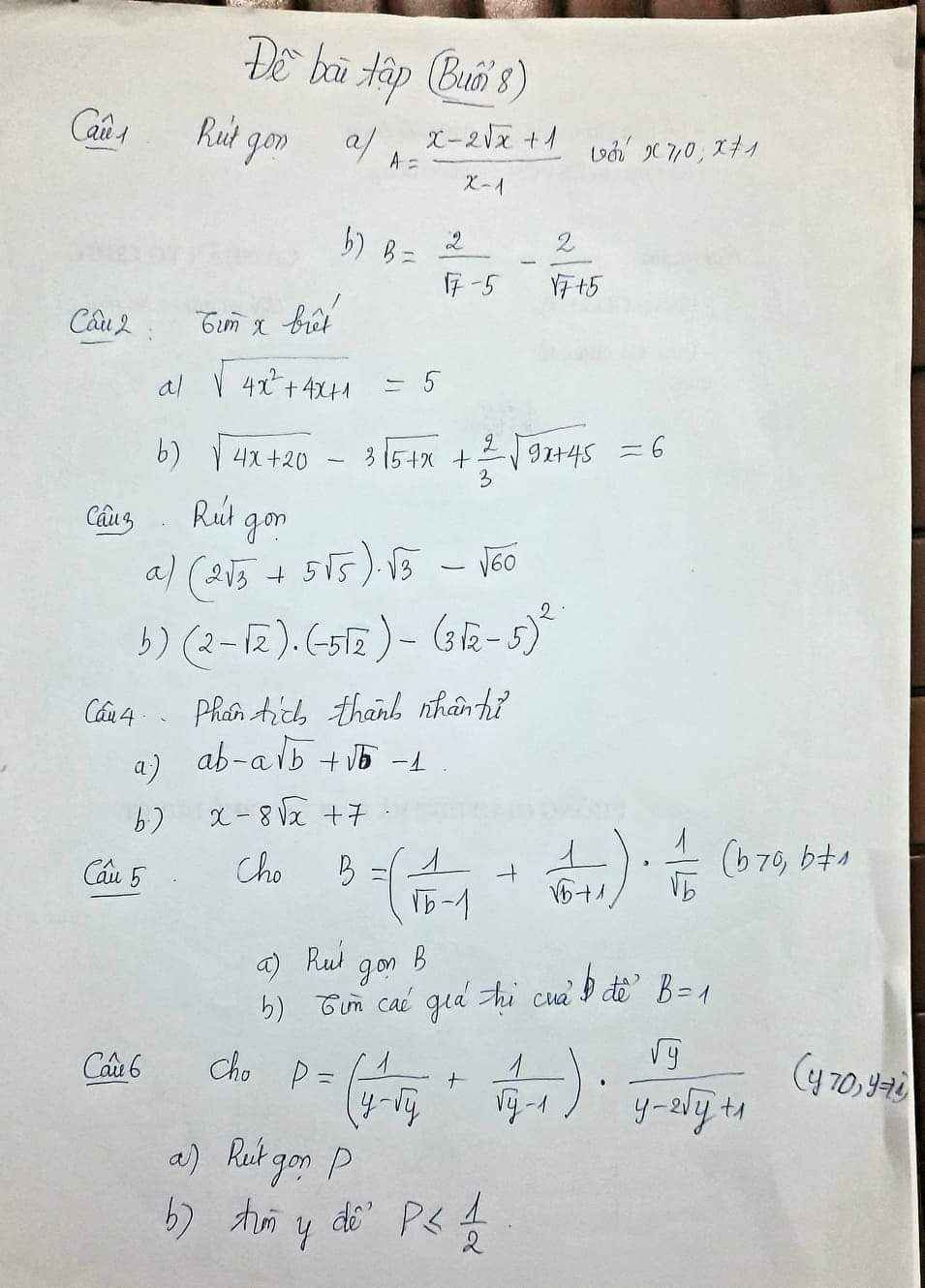Câu 1:
a) \(A=\dfrac{x-2\sqrt{x}+1}{x-1}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b) \(B=\dfrac{2}{\sqrt{7}-5}-\dfrac{2}{\sqrt{7}+5}=\dfrac{2\left(\sqrt{7}+5\right)-2\left(\sqrt{7}-5\right)}{\left(\sqrt{7}-5\right)\left(\sqrt{7}+5\right)}=-\dfrac{20}{18}=-\dfrac{10}{9}\)
Câu 2:
a) \(\sqrt{4x^2+4x+1}=5\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=5\)
\(\Leftrightarrow2x+1=5\)
\(\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
b) \(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{2}{3}\sqrt{9x+45}=6\)
\(\Leftrightarrow2\sqrt{5+x}-3\sqrt{5+x}+2\sqrt{5+x}=6\)
\(\Leftrightarrow\sqrt{5+x}=6\)
\(\Leftrightarrow\left\{{}\begin{matrix}5+x\ge0\\5+x=36\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-5\\x=31\end{matrix}\right.\) \(\Leftrightarrow x=31\)
Vậy \(S=\left\{31\right\}\)
câu 1
a) A=\(\dfrac{x-2\sqrt{x}+1}{x-1}\)=\(\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b) B=\(\dfrac{2\left(\sqrt{7}+5\right)-2\left(\sqrt{7}-5\right)}{\left(\sqrt{7}-5\right)\left(\sqrt{7}+5\right)}\)=\(\dfrac{2\sqrt{7}+10-2\sqrt{7}+10}{7-25}\)
=\(\dfrac{-20}{18}\)=\(\dfrac{-10}{9}\)
câu 2
a)\(\sqrt{4x^2+4x+1}\)=5\(\Rightarrow\)\(\sqrt{\left(2x+1\right)^2}\)=5\(\Rightarrow\)2x+1=5\(\Rightarrow\)x=2
b)\(\Rightarrow\)\(\sqrt{4\left(x+5\right)}\)-\(3\sqrt{5+x}\)+\(\dfrac{2}{3}\)\(\sqrt{9\left(x+5\right)}\)=5
\(\Rightarrow\)\(2\sqrt{x+5}\)-3\(\sqrt{5+x}\)+\(2\sqrt{x+5}\)=5
\(\Rightarrow\)\(\sqrt{x+5}\)=5\(\Rightarrow\)x+5=25\(\Rightarrow\)x=20
câu 3
a)\(\left(2\sqrt{3}+5\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)=6+\(5\sqrt{15}\)-\(2\sqrt{15}\)=6+\(3\sqrt{15}\)
b)\(\left(2-\sqrt{2}\right)\left(-5\sqrt{2}\right)-\left(3\sqrt{2}-5\right)^2\)
=\(-10\sqrt{2}+10-18+30\sqrt{2}\)\(-25\)=\(20\sqrt{2}-33\)
Câu 3:
a) \(\left(2\sqrt{3}+5\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)
\(=6+5\sqrt{15}-2\sqrt{15}\)
\(=6+3\sqrt{15}\)
b) \(\left(2-\sqrt{2}\right)\left(-5\sqrt{2}\right)-\left(3\sqrt{2}-5\right)^2\)
\(=10-10\sqrt{2}-18+30\sqrt{2}-25\)
\(=20\sqrt{2}-33\)
Câu 4:
a) \(ab-a\sqrt{b}+\sqrt{b}-1\)
\(=a\sqrt{b}\left(\sqrt{b}-1\right)+\sqrt{b}-1\)
\(=\left(a\sqrt{b}+1\right)\left(\sqrt{b}-1\right)\)
b) \(x-8\sqrt{x}+7\)
\(=x-\sqrt{x}-7\sqrt{x}+7\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-7\left(\sqrt{x}-1\right)\)
\(=\left(\sqrt{x}-1\right)\left(\sqrt{x}-7\right)\)
Câu 5:
a) \(B=\left(\dfrac{1}{\sqrt{b}-1}+\dfrac{1}{\sqrt{b}+1}\right)\dfrac{1}{\sqrt{b}}\)
\(=\dfrac{\sqrt{b}+1+\sqrt{b}-1}{\left(\sqrt{b}+1\right)\left(\sqrt{b}-1\right)}\) \(=\dfrac{2\sqrt{b}}{b-1}.\dfrac{1}{\sqrt{b}}=\dfrac{2}{b-1}\)
b) \(B=1\Leftrightarrow\dfrac{2}{b-1}=1\) (*)
ĐKXĐ: \(b-1\ne0\Leftrightarrow b\ne1\)
(*) \(\Leftrightarrow b-1=2\) \(\Leftrightarrow b=3\)
Vậy để \(B=1\) thì \(b=3\)
câu 4
a)=\(a\sqrt{b}\left(\sqrt{b}-1\right)+\left(\sqrt{b}-1\right)\)=\(\left(\sqrt{b}-1\right)\left(a\sqrt{b}+1\right)\)
b)=\(x-\sqrt{x}-7\sqrt{x}+7\)=\(\sqrt{x}\left(\sqrt{x}-1\right)-7\left(\sqrt{x}-1\right)\)
=\(\left(\sqrt{x}-1\right)\left(\sqrt{x}-7\right)\)
câu 5
a) B=\(\dfrac{\sqrt{b}+1+\sqrt{b}-1}{\left(\sqrt{b}-1\right)\left(\sqrt{b}+1\right)}\).\(\dfrac{1}{\sqrt{b}}\)=\(\dfrac{2\sqrt{b}}{b-1}.\dfrac{1}{\sqrt{b}}\)=\(\dfrac{2}{b-1}\)
b) để B=1\(\Rightarrow\)\(\dfrac{2}{b-1}=1\)\(\Rightarrow\)2=b-1
\(\Rightarrow\)b=3
câu 6
a) P=\(\left[\dfrac{1}{\sqrt{y}\left(\sqrt{y}-1\right)}+\dfrac{1}{\sqrt{y}-1}\right]\dfrac{\sqrt{y}}{\left(\sqrt{y}-1\right)^2}\)
P=\(\dfrac{1+\sqrt{y}}{\sqrt{y}\left(\sqrt{y}-1\right)}.\dfrac{\sqrt{y}}{\sqrt{y}-1}\)=\(\dfrac{1+\sqrt{y}}{\left(\sqrt{y}-1\right)^2}\)