10. \(a^4+b^4\ge\dfrac{\left(a+b\right)^4}{8}=\dfrac{1}{8}\left(S\text{vác}\right)\)
Dấu "=" \(\Leftrightarrow a=b=\dfrac{1}{2}\)
11. \(\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)=1+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{ab}\)
\(=1+\dfrac{2}{ab}\)
Ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\left(S\text{vác}\right)\)
\(\Rightarrow\dfrac{1}{ab}\ge4\Rightarrow ab\le\dfrac{1}{4}\)
Thay vào:
\(=1+\dfrac{2}{ab}\ge1+8=9\)
Dấu "=" \(\Leftrightarrow a=b=\dfrac{1}{2}\)
















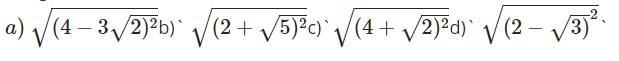




 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn