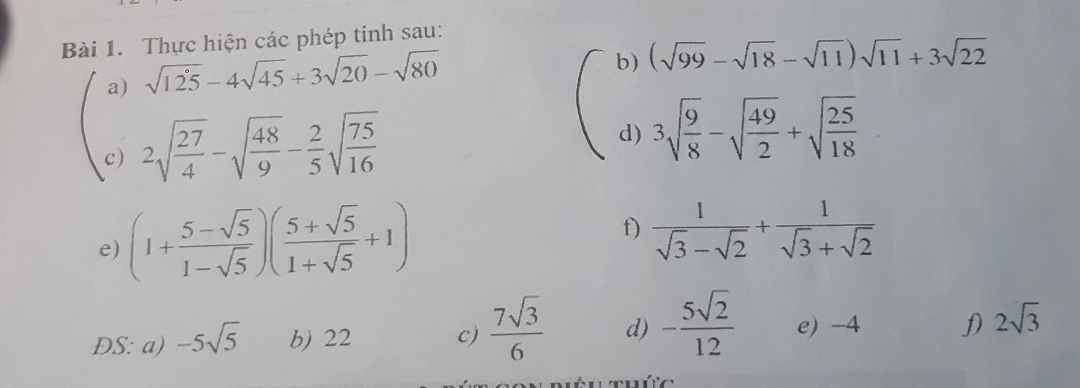a.
\(\sqrt{125}-4\sqrt{45}+3\sqrt{20}-\sqrt{80}=\sqrt{5^2.5}-4\sqrt{5.3^2}+3\sqrt{5.2^2}-\sqrt{5.4^2}\)
\(=5\sqrt{5}-4.3\sqrt{5}+3.2\sqrt{5}-4\sqrt{5}=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}\)
\(=(5-12+6-4)\sqrt{5}=-5\sqrt{5}\)
b.
\(=(\sqrt{3^2.11}-\sqrt{2.3^2}-\sqrt{11}).\sqrt{11}+3\sqrt{22}\)
\(=(3\sqrt{11}-3\sqrt{2}-\sqrt{11}).\sqrt{11}+3\sqrt{22}=(2\sqrt{11}-3\sqrt{2})\sqrt{11}+3\sqrt{22}\)
\(=2.\sqrt{11}.\sqrt{11}-3.\sqrt{2}.\sqrt{11}+3\sqrt{22}=2.11-3\sqrt{22}+3\sqrt{22}=22\)
c.
\(=2\sqrt{(\frac{3}{2})^2.3}-\sqrt{(\frac{4}{3})^2.3}-\frac{2}{5}\sqrt{(\frac{5}{4})^2.3}\)
\(=2.\frac{3}{2}.\sqrt{3}-\frac{4}{3}\sqrt{3}-\frac{2}{5}.\frac{5}{4}\sqrt{3}=3\sqrt{3}-\frac{4}{3}\sqrt{3}-\frac{1}{2}\sqrt{3}\)
\(=(3-\frac{4}{3}-\frac{1}{2})\sqrt{3}=\frac{7}{6}\sqrt{3}\)
d.
\(=3\sqrt{(\frac{3}{2})^2.\frac{1}{2}}-\sqrt{7^2.\frac{1}{2}}+\sqrt{(\frac{5}{3})^2.\frac{1}{2}}\)
\(=3.\frac{3}{2}\sqrt{\frac{1}{2}}-7\sqrt{\frac{1}{2}}+\frac{5}{3}\sqrt{\frac{1}{2}}=\frac{-5}{6}\sqrt{\frac{1}{2}}\)