Bài 5:
\(2\left(3a-2b+c\right)=a-5b\)
\(\Rightarrow6a-4b+2c=a-5b\)
\(\Rightarrow5a+b+2c=0\)
\(\Rightarrow b=-5a-2c\)
\(f\left(-1\right).f\left(2\right)=\left(a-b+c\right)\left(4a+2b+c\right)\)
\(=\left[a-\left(-5a-2c\right)+c\right]\left[4a+2\left(-5a-2c\right)+c\right]\)
\(=\left(6a+3c\right)\left(-6a-3c\right)=-\left(6a+3c\right)^2\le0\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}6a+3c=0\\b=-5a-2c\end{matrix}\right.\Leftrightarrow a=-b=-\dfrac{1}{2}c\)

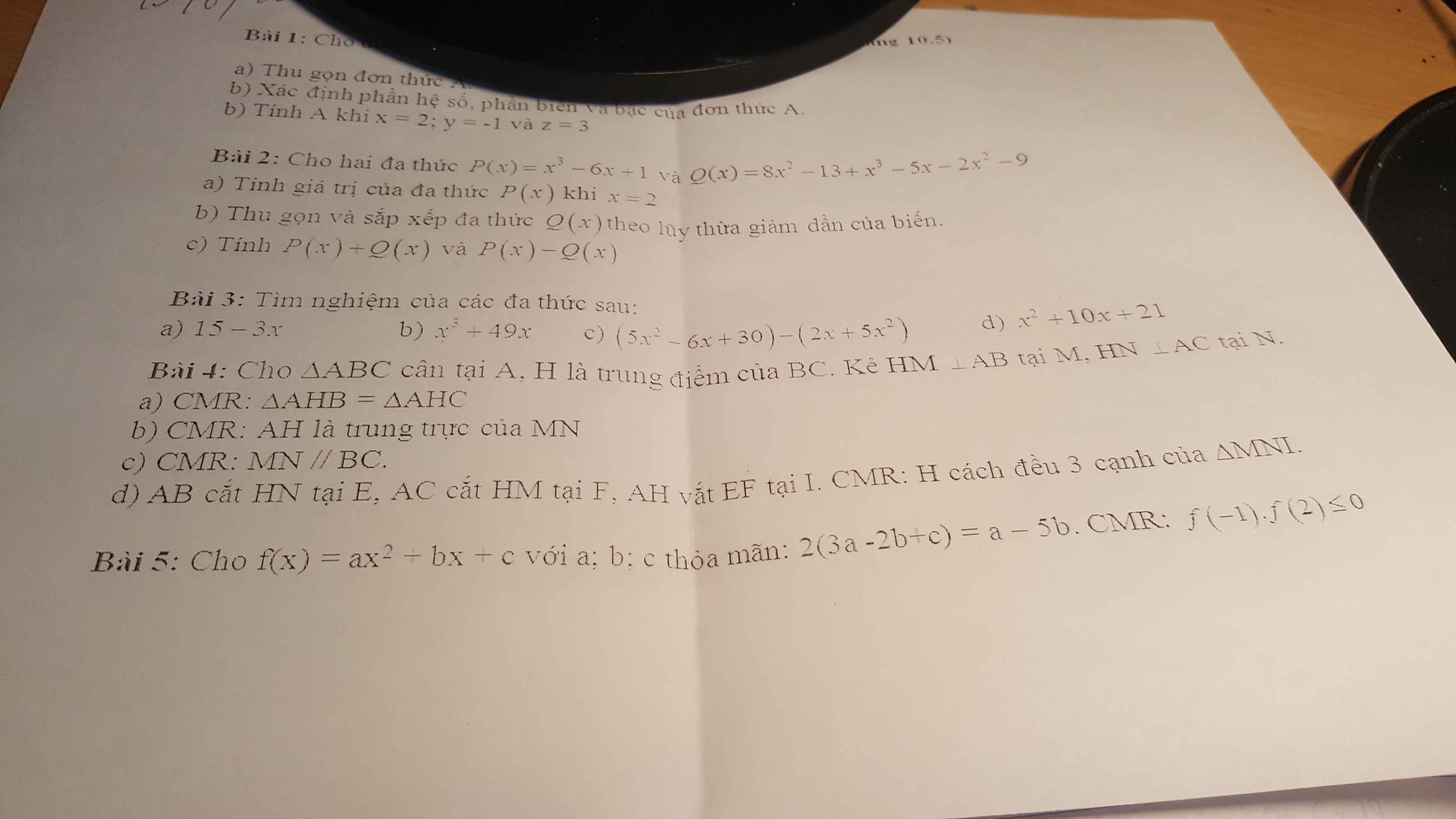






 giúp mik câu c bài 3 và hết bài 4 vs ạ
giúp mik câu c bài 3 và hết bài 4 vs ạ




 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé







