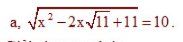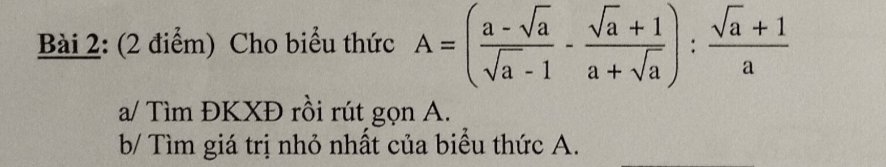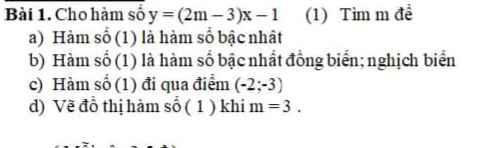7) \(x^4+\left(x^2+1\right)\sqrt{x^2+1}-1=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)+\left(x^2+1\right)\sqrt{x^2+1}=0\Leftrightarrow\left(x^2+1\right)\left(x^2-1+\sqrt{x^2+1}\right)=0\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(loại\right)\\x^2-1+\sqrt{x^2+1}=0\end{matrix}\right.\)
\(\Rightarrow x^2-1+\sqrt{x^2+1}=0\Leftrightarrow x^2+\dfrac{\left(\sqrt{x^2+1}-1\right)\left(\sqrt{x^2+1}+1\right)}{\sqrt{x^2+1}+1}=0\Leftrightarrow x^2+\dfrac{x^2}{\sqrt{x^2+1}+1}=0\Leftrightarrow x^2\left(1+\dfrac{1}{\sqrt{x^2+1}+1}\right)=0\Leftrightarrow x=0\)
vì \(1+\dfrac{1}{\sqrt{x^2+1}+1}>0\forall x\)
\(\Rightarrow x=0\)
8) \(x^2+2x\sqrt{x-\dfrac{1}{x}}=3x+1\) \(ĐKXĐ:x>1\)
\(\Leftrightarrow\left(x^2-x-1\right)+\left[2x\sqrt{\dfrac{x^2-1}{x}}-2x\right]=0\)
\(\Leftrightarrow\left(x^2-x-1\right)+2x\left(\sqrt{\dfrac{x^2-1}{x}}-1\right)=0\)
\(\Leftrightarrow\left(x^2-x-1\right)+\dfrac{2x\left(\sqrt{\dfrac{x^2-1}{x}}-1\right)\left(\sqrt{\dfrac{x^2-1}{x}}+1\right)}{\sqrt{\dfrac{x^2-1}{x}}+1}=0\)
\(\Leftrightarrow\left(x^2-x-1\right)+\dfrac{2x\left(\dfrac{x^2-1}{x}-1\right)}{\sqrt{\dfrac{x^2-1}{x}}+1}=0\Leftrightarrow\left(x^2-x-1\right)+\dfrac{2\left(x^2-x-1\right)}{\sqrt{\dfrac{x^2-1}{x}}+1}=0\)
\(\Leftrightarrow\left(x^2-x-1\right)\left(1+\dfrac{2}{\sqrt{\dfrac{x^2-1}{x}}+1}\right)=0\Leftrightarrow x^2-x-1=0\left(1+\dfrac{2}{\sqrt{\dfrac{x^2-1}{x}}+1}>0\forall x>1\right)\)
\(\Delta=\left(-1\right)^2-4\left(-1\right)=5\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{1+\sqrt{5}}{2}\left(tm\right)\) ; \(x_2=\dfrac{1-\sqrt{5}}{2}\left(loại\right)\)
\(\Rightarrow x=\dfrac{1+\sqrt{5}}{2}\)

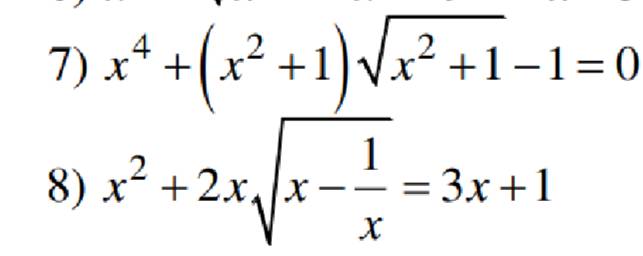





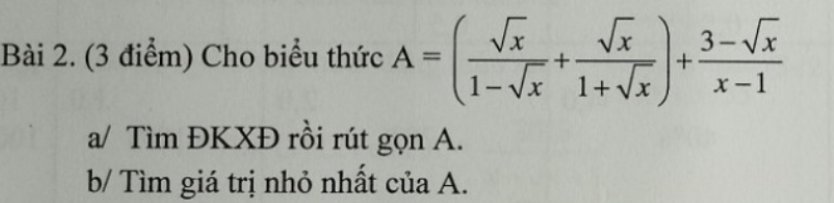


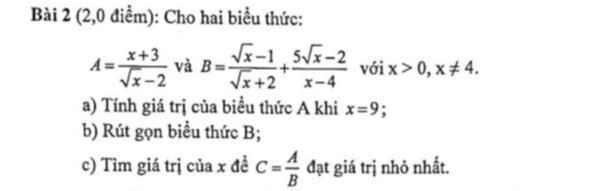 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ