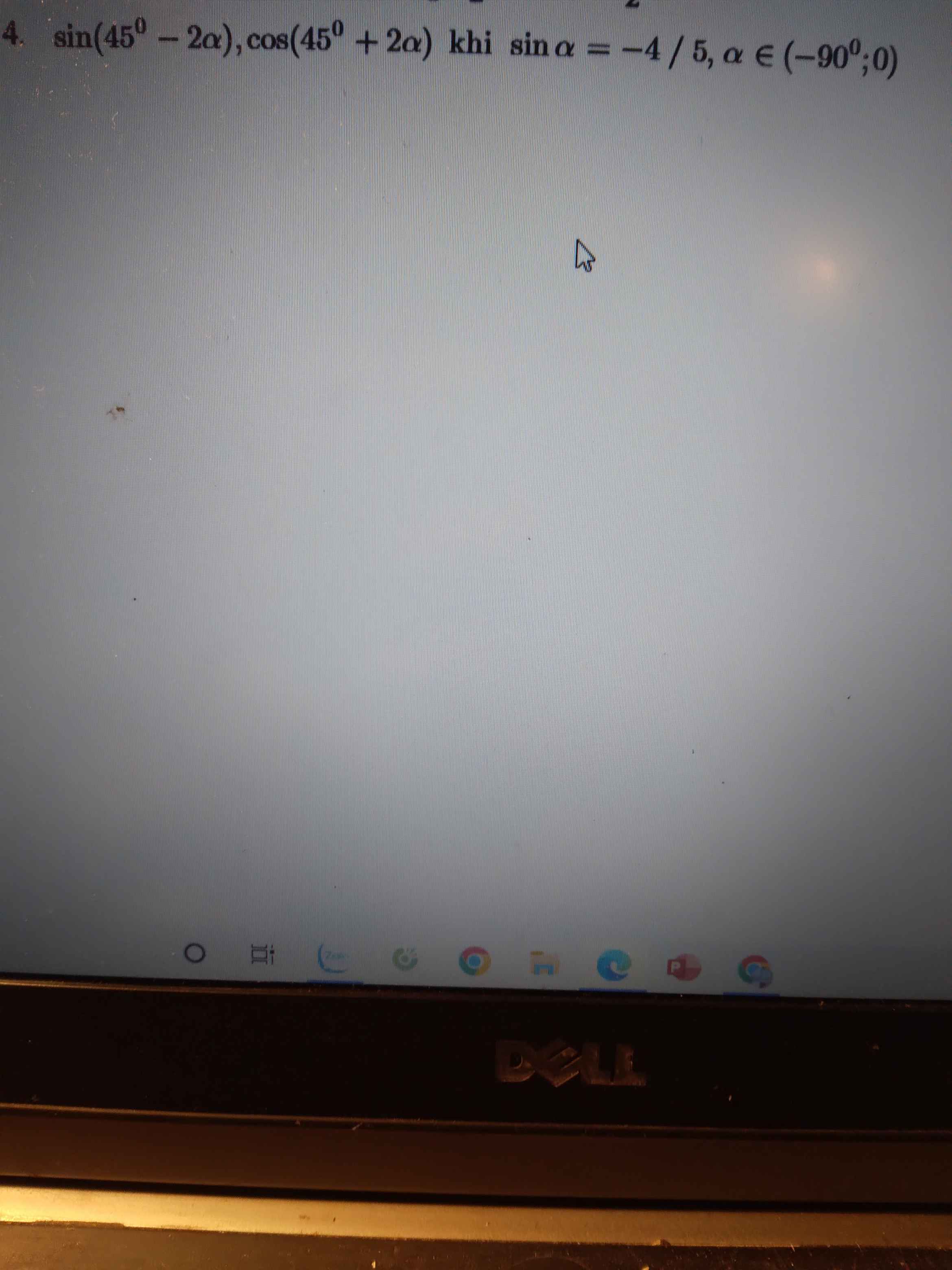
\(a\in\left(-90^0,0\right)\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{3}{5}\)
\(sin2a=2sina.cosa=-\dfrac{24}{25}\)
\(cos2a=2cos^2a-1=-\dfrac{7}{25}\)
\(sin\left(45^0-2a\right)=sin45^0.cos2a-cos45^0.sin2a=\dfrac{\sqrt{2}}{2}.\left(-\dfrac{7}{25}\right)-\dfrac{\sqrt{2}}{2}.\left(-\dfrac{24}{25}\right)=...\)
\(cos\left(45^0+2a\right)=cos45^0.cos2a-sin45^0.sin2a=\dfrac{\sqrt{2}}{2}.\left(-\dfrac{7}{25}\right)-\dfrac{\sqrt{2}}{2}.\left(-\dfrac{24}{25}\right)=...\)