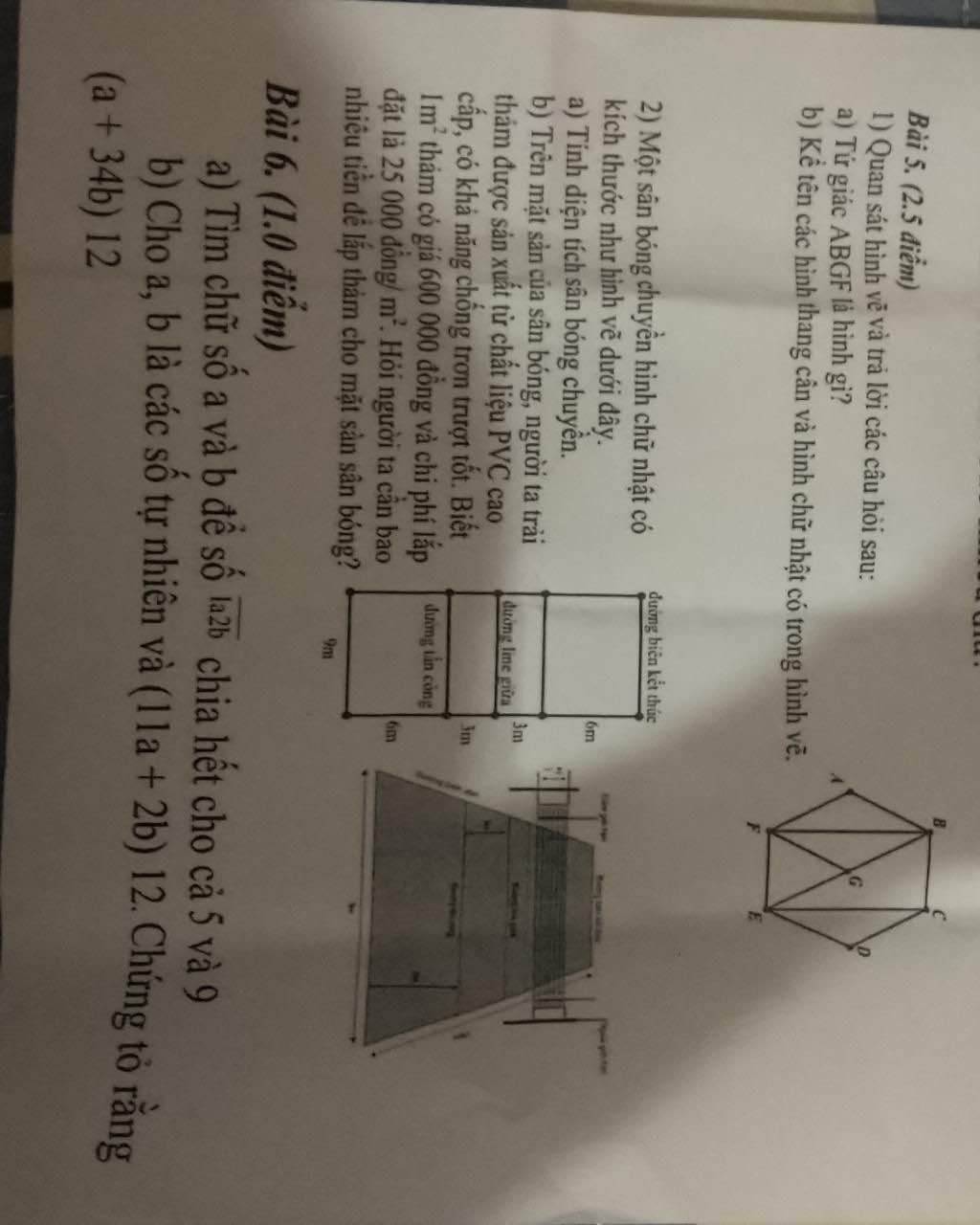
Lời giải:
$A> \frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{100.101}$
$A> \frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{101-100}{100.101}$
$A> \frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{100}-\frac{1}{101}$
$A> \frac{1}{5}-\frac{101}>\frac{1}{6}$
---------------
$A< \frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}$
$A< \frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}$
$A< \frac{1}{4}-\frac{1}{100}< \frac{1}{4}$

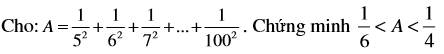





 giải giúp tui với ạ sắp đến h đi hc rùi cảm ơn nhìu
giải giúp tui với ạ sắp đến h đi hc rùi cảm ơn nhìu