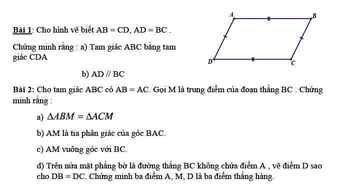
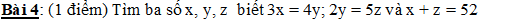Lời giải:
Nếu $x+y+z=0$ thì:
$\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=0$
$\Rightarrow x=y=z=0$ (thỏa mãn)
Nếu $x+y+z\neq 0$ thì áp dụng tính chất dãy tỉ số bằng nhau:
$x+y+z=\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=\frac{x+y+z}{y+z+1+x+z+2+x+y-3}=\frac{x+y+z}{2(x+y+z)}=\frac{1}{2}$
Khi đó:
Từ điều kiện $\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}$
$\Rightarrow \frac{x}{x+y+z+1}=\frac{y}{x+y+z+2}=\frac{z}{x+y+z-3}$
$\Leftrightarrow \frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}=\frac{x+y+z}{\frac{3}{2}+\frac{5}{2}+\frac{-5}{2}}=\frac{\frac{1}{2}}{\frac{3}{2}}=\frac{1}{3}$
$\Rightarrow x=\frac{1}{2}; y=\frac{5}{6}; z=\frac{-5}{6}$




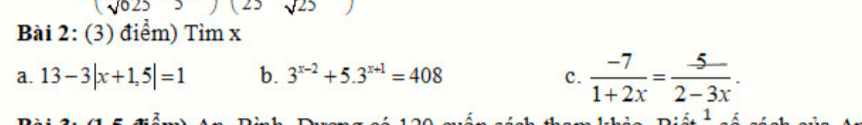

 giúp em câu 4,5,7 vs ạ em cảm ơn ;-;
giúp em câu 4,5,7 vs ạ em cảm ơn ;-;