Bài 1:
1. $2^n+2^{n+3}=144$
$2^n(1+2^3)=144$
$2^n.9=144$
$2^n=144:9=16=2^4\Rightarrow n=4$
2.
$3^n+3^{n+2}=270$
$3^n(1+3^2)=270$
$3^n.10=270$
$3^n=270:10=27=3^3\Rightarrow n=3$
3.
$2^n+2^{n+1}+2^{n+2}+2^{n+3}=960$
$2^n(1+2+2^2+2^3)=960$
$2^n.15=960$
$2^n=960:15=64=2^6$
$\Rightarrow n=6$
4.
$3^n+3^{n+1}+3^{n+2}+3^{n+3}=3240$
$3^n(1+3+3^2+3^3)=3240$
$3^n.40=3240$
$3^n=3240:40=81=3^4\Rightarrow n=4$
Bài 2:
1. $(x+1)^2=49=7^2$
$\Rightarrow x+1=7$
$\Rightarrow x=6$
2.
$(x+2)^3=512=8^3$
$\Rightarrow x+2=8\Rightarrow x=6$
3.
$(x-3)^9=(x-3)$
$\Rightarrow (x-3)^9-(x-3)=0$
$\Rightarrow (x-3)[(x-3)^8-1]=0$
$\Rightarrow x-3=0$ hoặc $(x-3)^8-1=0$
$\Rightarrow x-3=0$ hoặc $(x-3)^8=1=1^8=(-1)^8$
$\Rightarrow x=3$ hoặc $x-3=1$ hoặc $x-3=-1$
$\Rightarrow x=3$ hoặc $x=4$ hoặc $x=2$
Bài 2:
4. $(x-5)^{20}=(x-5)^{11}$
$(x-5)^{20}-(x-5)^{11}=0$
$(x-5)^{11}[(x-5)^9-1]=0$
$\Rightarrow (x-5)^{11}=0$ hoặc $(x-5)^9-1=0$
$\Rightarrow (x-5)^{11}=0$ hoặc $(x-5)^9=1$
$\Rightarrow x-5=0$ hoặc $x-5=1$
$\Rightarrow x=5$ hoặc $x=6$
5.
$(x-6)^{2023}-(x-6)^{2012}=0$
$(x-6)^{2012}[(x-6)^{11}-1]=0$
$\Rightarrow (x-6)^{2012}=0$ hoặc $(x-6)^{11}-1=0$
$\Rightarrow x-6=0$ hoặc $x-6=1$
$\Rightarrow x=6$ hoặc $x=7$.
Bài 3:
1. $7^x=38-11^y< 38< 49=7^2$
$\Rightarrow x< 2$. Do đó $x=0$ hoặc $x=1$.
Nếu $x=0$ thì: $11^y=38-7^x=38-7^0=37$
$\Rightarrow y\not\in\mathbb{N}$ (loại)
Vậy không tồn tại $x,y$ thỏa đề.
2.
$(x+1)^2+4^y=65$
$4^y=65-(x+1)^2\leq 64$ với mọi $x\in\mathbb{N}$
$\Rightarrow 4^y\leq 4^3\Rightarrow y\leq 3$
$\Rightarrow y=0,1,2,3$
Nếu $y=0$ thì: $(x+1)^2=65-4^0=64$
$\Rightarrow x+1=8$ (do $x+1>0$)
$\Rightarrow x=7$
Nếu $y=1$ thì: $(x+1)^2=65-4^1=61$ (không là scp - loại)
Nếu $y=2$ thì $(x+1)^2=65-4^2=49$
$\Rightarrow x+1=7$ (do $x+1>0$)
$\Rightarrow x=6$
Nếu $y=3$ thì $(x+1)^2=65-4^3=1$
$\Rightarrow x+1=1$ (do $x+1>0$)
$\Rightarrow x=0$
Bài 3:
3.
$13^x+8^y=177$
Nếu $x\geq 3$ thì $13^x\geq 13^3>177$
$\Rightarrow 13^x+8^y> 177$ (trái với đề - loại)
$\Rightarrow x< 3\Rightarrow x=0,1,2$
Nếu $x=0$ thì:
$8^y=177-13^0=176$
$\Rightarrow y\not\in\mathbb{N}$ (loại)
Nếu $x=1$ thì:
$8^y=177-13^1=164$
$\Rightarrow y\not\in\mathbb{N}$ (loại)
Nếu $x=2$ thì:
$8^y=177-13^2=8$
$\Rightarrow y=1$
Vậy $x=2; y=1$
4.
$(x-2)^2+5^y=29$
Nếu $y\geq 3$ thì $5^y\geq 5^3> 29$
$\Rightarrow (x-2)^2+5^y> 29$ (trái với đề - loại)
$\Rightarrow y< 3$. Do đó $y=0,1,2$
Nếu $y=0$ thì: $(x-2)^2=29-5^0=28$ không là scp (loại)
Nếu $y=1$ thì $(x-2)^2=29-5^1=24$ không phải scp (loại)
Nếu $y=2$ thì $(x-2)^2=29-5^2=4$
$\Rightarrow x-2=2$ hoặc $x-2=-2$
$\Rightarrow x=4$ hoặc $x=0$
Bài 4:
1.
$(x-1)(y-2)=23$. Với $x,y$ tự nhiên thì $x-1, y-2$ là số nguyên. Khi đó ta có các TH sau:
TH1: $x-1=1; y-2=23$
$\Rightarrow x=2; y=25$ (tm)
TH2: $x-1=-1, y-2=-23$
$\Rightarrow x=0; y=-21$ (loại do $y$ là stn)
TH3: $x-1=-23, y-2=-1$
$\Rightarrow x=-22$ (loại do $x$ là stn)
TH4: $x-1=23; y-2=1$
$\Rightarrow x=24; y=3$ (tm)
2. Do $x,y$ là stn nên $x-2, y-3$ là số nguyên. Mà $(x-2)(y-3)=47$ nên có thể có các TH sau:
TH1: $x-2=1; y-3=47\Rightarrow x=3; y=50$ (tm)
TH2: $x-2=-1; y-3=-47\Rightarrow x=1; y=-44$ (loại do $y$ là stn)
TH3: $x-2=-47; y-3=-1\Rightarrow x=-45$ (loại do $x$ là stn)
TH4: $x-2=47; y-3=1\Rightarrow x=49; y=4$ (tm)
Bài 4:
3.
$x(y+1)=29$ mà $x,y+1$ là số tự nhiên với mọi $x,y$ là stn nên ta xét các TH sau:
TH1: $x=29; y+1=1\Rightarrow x=29; y=0$ (tm)
TH2: $x=1, y+1=29\Rightarrow x=1; y=28$ (tm)
4.
$x+xy=31$
$x(1+y)=31$
Do $x,y+1$ là stn với mọi $x,y$ là stn nên xét các TH sau:
TH1: $x=1, y+1=31\Rightarrow x=1; y=30$
TH2: $x=31; y+1=1\Rightarrow x=31; y=0$






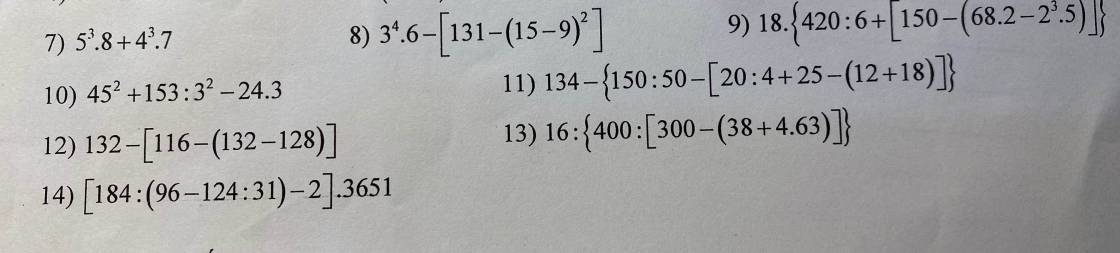

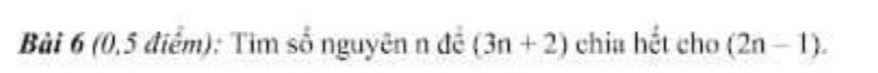 mn giúp em với ạ, em đang cần gấp lắm ạ
mn giúp em với ạ, em đang cần gấp lắm ạ




 các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
các bạn giúp mik trc 7h tối nay nha. Mik tick cho bạn nào nhanh và đúng nhé
