1.
a.
\(n^2+7n+1=k^2\Rightarrow4n^2+28n+4=4k^2\)
\(\Leftrightarrow\left(2n+7\right)^2-45=\left(2k\right)^2\)
\(\Leftrightarrow\left(2n-2k+7\right)\left(2n+2k+7\right)=45\)
Phương trình ước số cơ bản
b.
\(a^3b^3+b^3-3ab^2=-1\)
\(\Leftrightarrow a^3+1-\dfrac{3a}{b}=-\dfrac{1}{b^3}\)
\(\Leftrightarrow a^3+\dfrac{1}{b^3}+1-\dfrac{3a}{b}=0\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x^3+y^3+1-3xy=0\)
\(\Leftrightarrow\left(x+y\right)^3+1-3xy\left(x+y\right)-3xy=0\)
\(\Leftrightarrow\left(x+y+1\right)\left(x^2+y^2+1-xy-x-y\right)=0\)
\(\Leftrightarrow x+y+1=0\)
\(\Rightarrow P=a+\dfrac{1}{b}=x+y=-1\)
2.
a.
\(a+b+\dfrac{1}{a}+\dfrac{1}{b}=\left(\dfrac{a}{4}+\dfrac{1}{a}\right)+\left(\dfrac{b}{4}+\dfrac{1}{b}\right)+\dfrac{3}{4}\left(a+b\right)\)
\(\ge2\sqrt{\dfrac{a}{4a}}+2\sqrt{\dfrac{b}{4b}}+\dfrac{3}{4}.4=5\) (đpcm)
Dấu "=" xảy ra khi \(a=b=2\)
2.b
b.
\(\Leftrightarrow x^4+4x+4=y^4+4y+4\)
\(\Leftrightarrow\left(x+2\right)^2=y^4+4y+4\)
\(\Rightarrow y^4+4y+4\) là số chính phương
Ta có: \(y^4+4y+4>y^4\) với mọi y nguyên dương
\(y^4+4y+4\le y^4+4y^2+4=\left(y^2+2\right)^2\)
\(\Rightarrow\left(y^2\right)^2< y^4+4y+4\le\left(y^2+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}y^4+4y+4=\left(y^2+1\right)^2\\y^4+4y+4=\left(y^2+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2y^2-4y-3=0\left(ktm\right)\\y^2-y=0\Rightarrow y=1\end{matrix}\right.\)
Thế vào pt ban đầu \(\Rightarrow x^2+4x=5\Rightarrow x=1\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
3.
a.
\(\left(a^3+1+1\right)+\left(b^3+1+1\right)+\left(c^3+1+1\right)\ge3a+3b+3c=9\)
\(\Rightarrow a^3+b^3+c^3+6\ge9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
Dấu "=" xảy ra khi \(a=b=c=1\)
b.
\(\dfrac{a}{a^3+bc+2}=\dfrac{a}{a^3+1+1+bc}\le\dfrac{a}{3a+bc}=\dfrac{a}{a\left(a+b+c\right)+bc}=\dfrac{a}{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}\right)\)
Tương tự:
\(\dfrac{b}{b^3+ac+2}\le\dfrac{1}{4}\left(\dfrac{b}{a+b}+\dfrac{b}{b+c}\right)\) ; \(\dfrac{c}{c^3+ab+2}\le\dfrac{1}{4}\left(\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\)
Cộng vế:
\(VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{b}{a+b}+\dfrac{a}{a+c}+\dfrac{c}{a+c}+\dfrac{b}{b+c}+\dfrac{c}{b+c}\right)=\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Mọi người ơi giúp em với ạ, em đang cần gấp, thanks mn
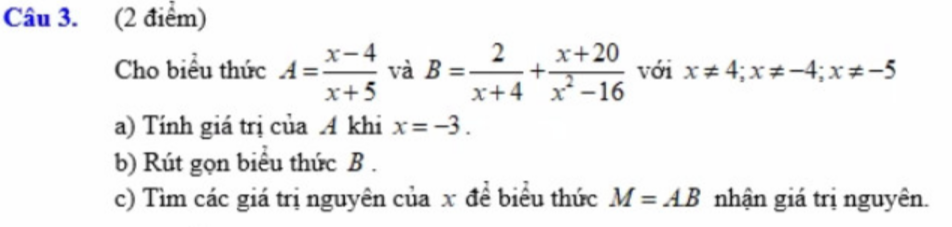
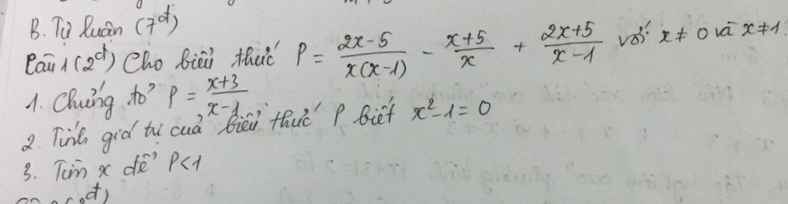mọi người giúp em với ạ , em đang cần gấp :))