ĐK : x \(\ge-1\)
Ta có : \(x^2-2x-1=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
<=> \(\left(x^2+1\right)-2\left(x+1\right)=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
Đặt \(\sqrt{x^2+1}=a;\sqrt{x+1}=b\)(\(a>0;b\ge0\))
Khi đó a2 - 2b2 = ab
<=> (a - 2b)(a + b) = 0
<=> a - 2b = 0
<=> a = 2b
<=> \(\sqrt{x^2+1}=2\sqrt{x+1}\)
<=> \(\left\{{}\begin{matrix}x^2+1=4x+4\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-3=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{7}+2\\x=-\sqrt{7}+2\end{matrix}\right.\\x\ge-1\end{matrix}\right.\Leftrightarrow x=\sqrt{7}+2\)

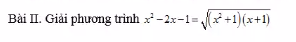








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp