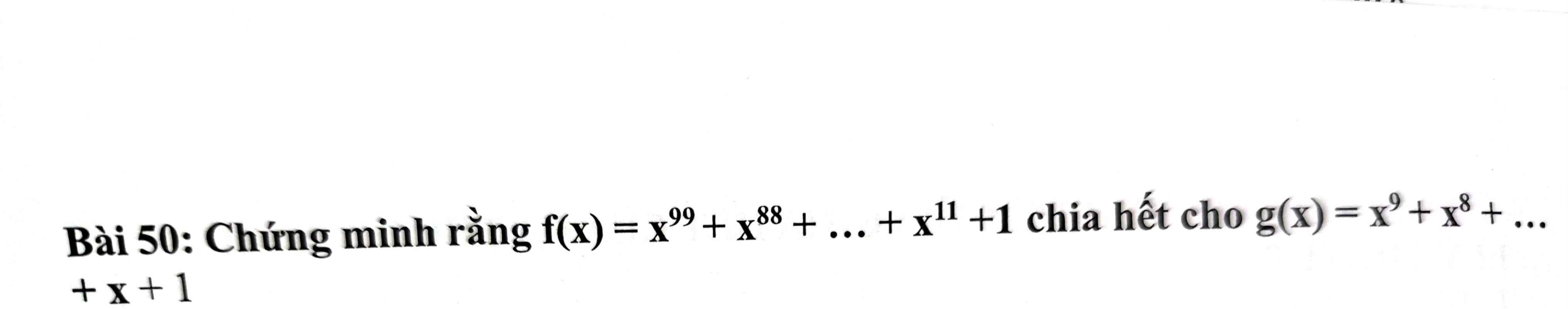Question

  giúp em với ạ

Bài 50: Chứng minh rằng \( f(x) = x^{99} + x^{88} + \ldots + x^{11} + 1 \) chia hết cho \( g(x) = x^9 + x^8 + \ldots + x + 1 \)

Answer 1

Ta có: `f(x) -g(x)=(x^99+x^88+...+x^11+1)-(x^9+x^8+...+x+1)`

`=(x^99-x^9)+(x^88-x^8)+...+(x^11-x)`

`=x^9(x^90-1)+x^8(x^80-1)+...+x(x^10-1)`

Ta có:`x^90-1=(x^10)^9-1^9 \vdots x^10-1` (vì `a^n-b^n \vdots a-b`)

`=> x^80-1 \vdots x^10-1,....,x^10-1 \vdots x^10-1`

`=> f(x)-g(x) \vdots x^10-1`

mà `x^10-1=(x^10+x^9+x^8+...+x^2+x) - (x^9+x^8+...+x+1)=(x-1)(x^9+x^8+...+1)`

`=> x^10-1 \vdots g(x)`

`=> f(x)-g(x) \vdots g(x)`

`=> f(x) \vdots g(x)`    `(đpcm)`