6.
a. Đúng, theo tính chất trọng tâm
b. Đúng
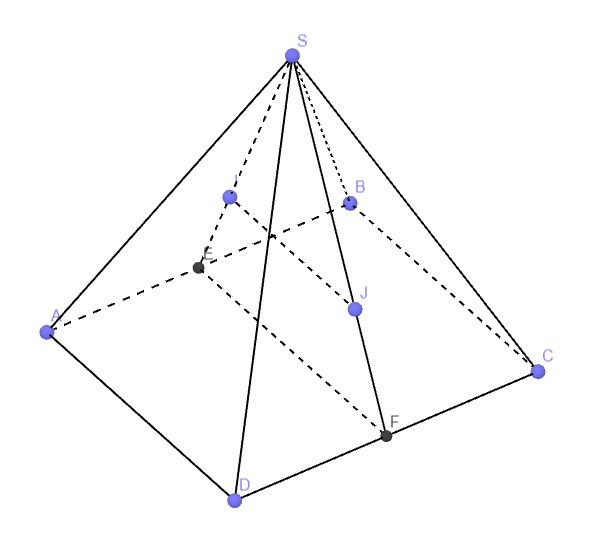
Do I là trọng tâm tam giác SAB nên \(\dfrac{SI}{SE}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{SI}{SE}=\dfrac{SJ}{SF}=\dfrac{2}{3}\Rightarrow IJ||EF\) (1) theo định lý Thales đảo
\(\Rightarrow IJ||\left(ABCD\right)\)
c. Đúng
\(ABCD\) là hbh \(\Rightarrow BC||AD\Rightarrow BC||\left(SAD\right)\)
E là trung điểm AB, F là trung điểm CD \(\Rightarrow EF||AD||BC\) (2)
\(\Rightarrow BC||\left(SEF\right)\)
d. Sai
Từ (1) và (2) \(\Rightarrow BC||IJ\)
\(\Rightarrow BC||\left(AIJ\right)\)
7.
a. Đúng
b. Sai
Mệnh đề đúng là: nếu mặt phẳng này chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng kia thì hai mặt phẳng song song
c. Sai
Có thể là hai mặt phẳng trùng nhau.
Mệnh đề đúng là: hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
d. Sai
Hiển nhiên rồi, ví dụ hai mặt phẳng cắt nhau theo giao tuyến d và d song song với d' bất kì
8.
a. Đúng
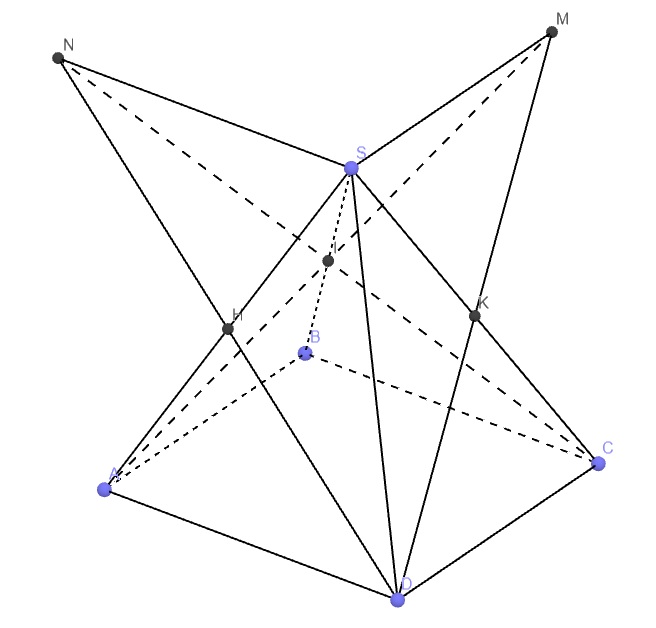
H là trung điểm SA, I là trung điểm SB nên HI là đường trung bình tam giác SAB
\(\Rightarrow HI||AB\Rightarrow HI||\left(ABCD\right)\) (1)
b. Đúng
Tương tự câu a ta có IK là đường trung bình tam giác SBC
\(\Rightarrow IK||BC\Rightarrow IK||\left(ABCD\right)\) (2)
Mà IK cắt HI tại I (3)
(1);(2);(3) \(\Rightarrow\left(HIK\right)||\left(ABCD\right)\)
c. Sai
\(\left\{{}\begin{matrix}M\in AI\in\left(SAB\right)\\M\in DK\in\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow M\in\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SM=\left(SAB\right)\cap\left(SCD\right)\)
\(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\end{matrix}\right.\) \(\Rightarrow\left(SAB\right)\cap\left(SCD\right)=SM||AB||CD\)
Mà \(HI||AB\) theo cm câu a
\(\Rightarrow SM||HI\)
d. Sai
Chứng minh tương tự câu c ta có \(SN=\left(SAD\right)\cap\left(SBC\right)\)
Mà \(AD||BC\Rightarrow SN||AD||BC\Rightarrow SN||\left(ABCD\right)\) (4)
Theo câu c \(SM||AB\Rightarrow SM||\left(ABCD\right)\) (5)
(4);(5) \(\Rightarrow\left(SMN\right)||\left(ABCD\right)\)
Kết hợp câu b \(\left(HIK\right)||\left(ABCD\right)\Rightarrow\left(SMN\right)||\left(HIK\right)\)
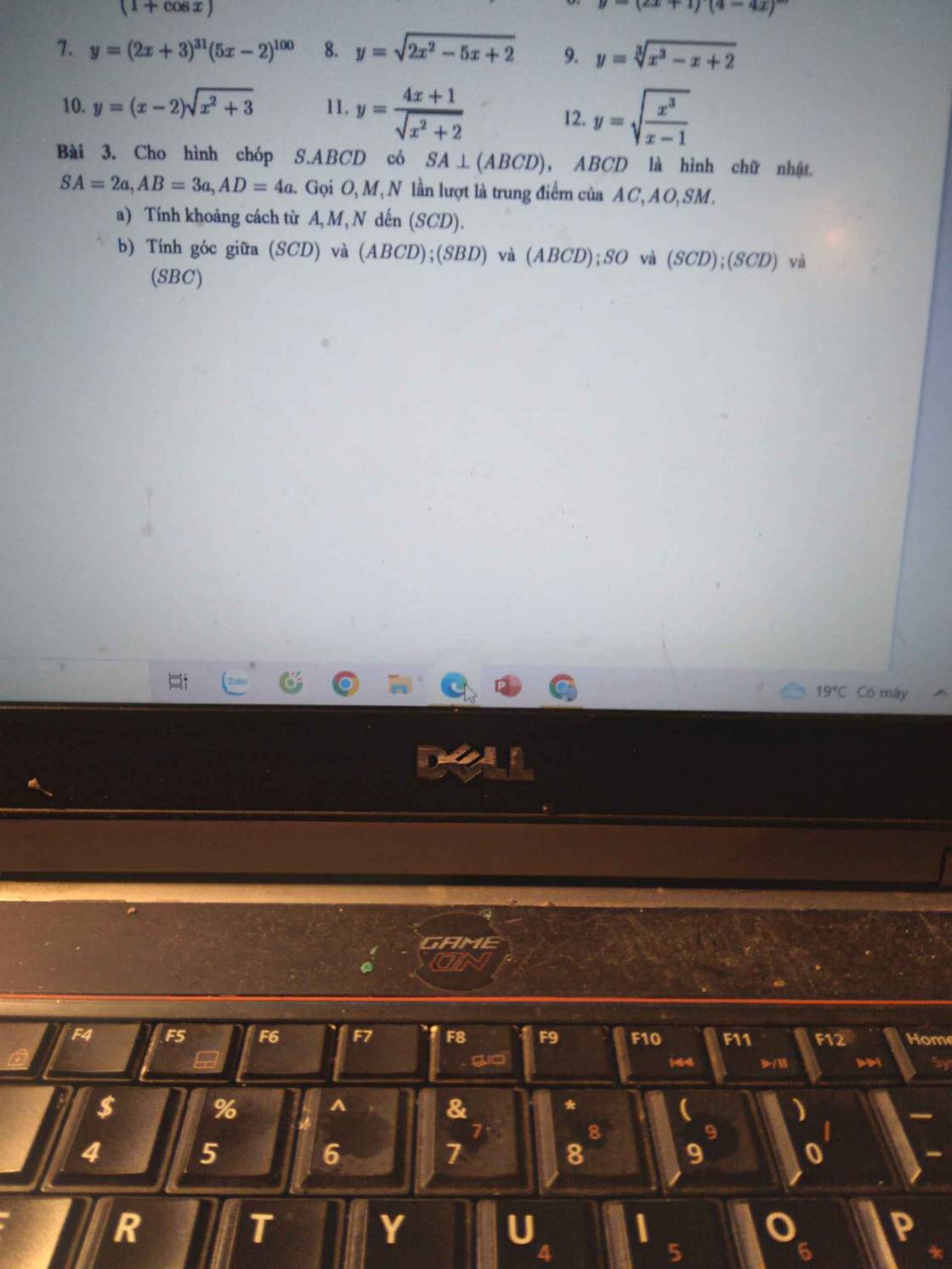Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
