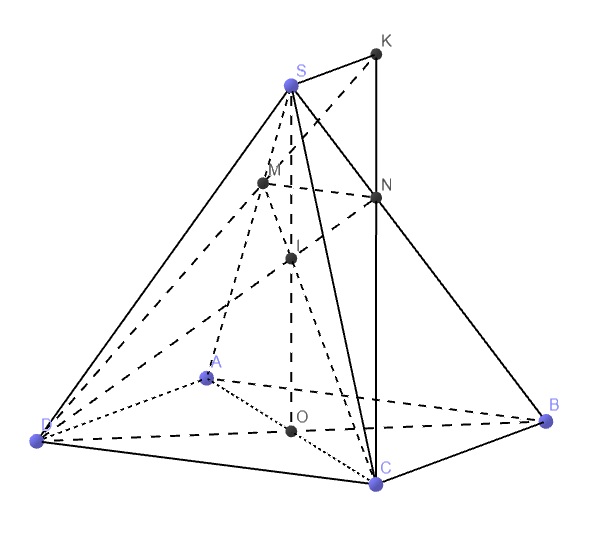
7.
a. Đúng
Theo giả thiết thì \(\left(ICD\right)\cap SA=M\)
b. Sai
I là trung điểm SO \(\Rightarrow SI=IO\)
O là trung điểm BD \(\Rightarrow\dfrac{OD}{DB}=\dfrac{1}{2}\)
Áp dụng định lý Menelaus trong tam giác SBO:
\(\dfrac{SI}{IO}.\dfrac{OD}{DB}.\dfrac{BN}{NS}=1\Leftrightarrow1.\dfrac{1}{2}.\dfrac{BN}{NS}=1\Rightarrow BN=2NS\)
\(\Rightarrow SB-SN=2SN\)
\(\Rightarrow SN=\dfrac{1}{3}SB\)
c. Sai
Tương tự câu b ta có \(SM=\dfrac{1}{3}SA\)
\(\Rightarrow\dfrac{MN}{AB}=\dfrac{SM}{SA}=\dfrac{SN}{SN}=\dfrac{1}{3}\)
\(\Rightarrow MN=\dfrac{1}{3}AB=\dfrac{a}{3}\)
d. Sai
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
\(\left\{{}\begin{matrix}K\in CN\in\left(SBC\right)\\K\in DM\in\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow K\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
Mà \(AD||BC\Rightarrow SK||AD||BC\)
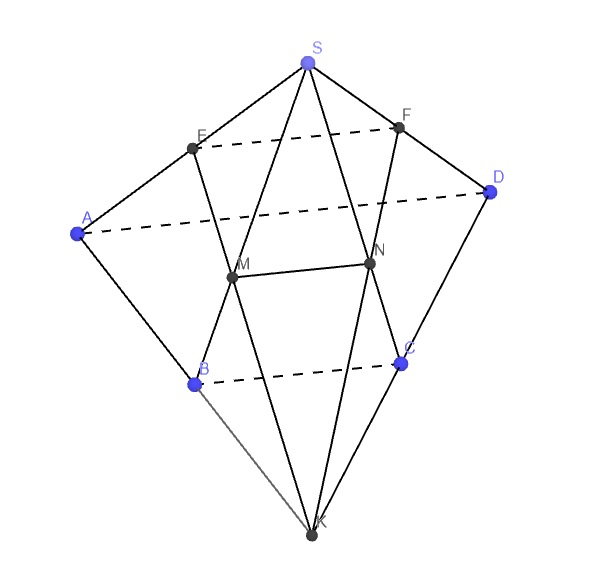
8.
a. Đúng
\(K\in CD\in\left(CDE\right)\Rightarrow KE\in\left(CDE\right)\)
\(KE\cap SB=M\)
\(\left\{{}\begin{matrix}M\in SB\\M\in KE\in\left(CDE\right)\end{matrix}\right.\) \(\Rightarrow M=SB\cap\left(CDE\right)\)
b.Sai
\(K\in EM\in\left(EFM\right)\)
\(KF\cap SC=N\Rightarrow N=SC\cap\left(EFM\right)\)
Do đó EM cắt FN tại K nên EFNM ko thể là hình bình hành (1 cặp cạnh đối ko song song mà cắt nhau)
c. Đúng
\(SK=\left(SAB\right)\cap\left(SCD\right)\)
\(AM=\left(ADNM\right)\cap\left(SAB\right)\)
\(DN=\left(ADNM\right)\cap\left(SCD\right)\)
Do đó 3 mặt phẳng (SAB), (SCD), (ADNM) cắt nhau theo 3 giao tuyến phân biệt là SK, AM, DN nên 3 đường thẳng này đồng quy
d. Sai
Do \(AD=2BC\Rightarrow BC\) là đường trung bình tam giác KAD
\(\Rightarrow B\) là trung điểm AK
\(\Rightarrow M\) là trọng tâm tam giác SAK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\)
Tương tự ta có N là trọng tâm tam giác SDK nên \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) \(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD nên \(EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{MN}{EF}=\dfrac{2}{3}\)
Hai tam giác KMN và KEF đồng dạng theo tỉ số \(k=\dfrac{MN}{EF}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=k^2=\dfrac{4}{9}\)
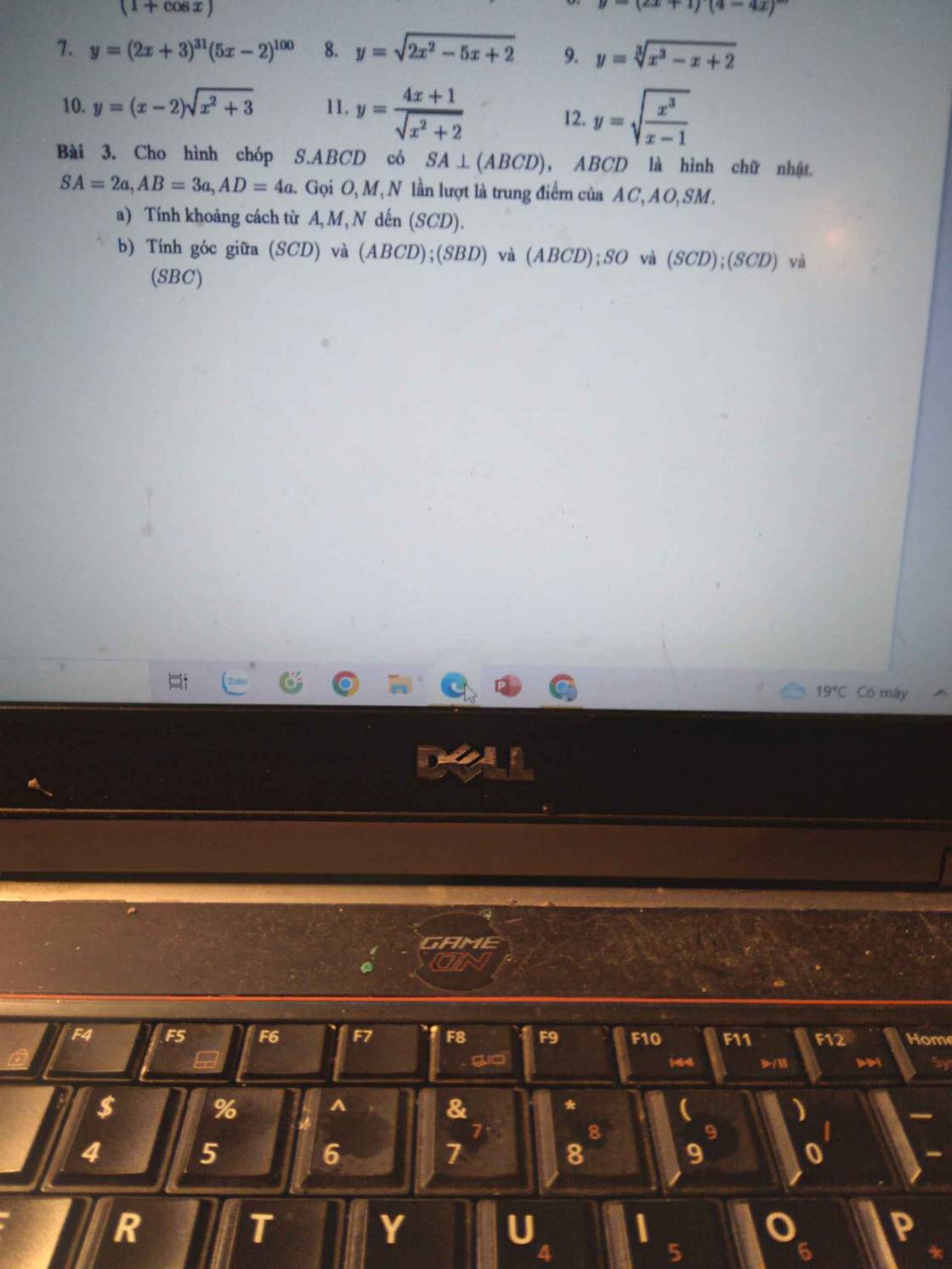Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
