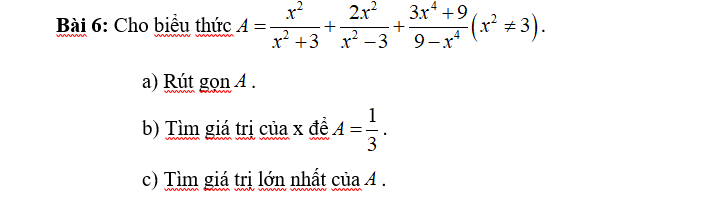a.
\(A=\dfrac{x^2}{x^2+3}+\dfrac{2x^2}{x^2-3}+\dfrac{3x^4+9}{9-x^4}\left(x^2\ne3\right)\)
\(A=\dfrac{x^2\left(x^2-3\right)}{\left(x^2+3\right)\left(x^2-3\right)}+\dfrac{2x^2\left(x^2+3\right)}{\left(x^2+3\right)\left(x^2-3\right)}-\dfrac{3x^4+9}{\left(x^2+3\right)\left(x^2-3\right)}\)
\(A=\dfrac{x^4-3x^2+2x^4+6x^2-3x^4-9}{\left(x^2+3\right)\left(x^2-3\right)}\)
\(A=\dfrac{3x^2-9}{\left(x^2+3\right)\left(x^2-3\right)}\)
\(A=\dfrac{3}{x^2+3}\)
b.
\(\dfrac{3}{x^2+3}=\dfrac{1}{3}\)
\(\Leftrightarrow x^2+3=9\)
\(\Leftrightarrow x^2=6\)
\(\Leftrightarrow x=\sqrt{6}\left(TM\right)\)
Đúng 1
Bình luận (0)
