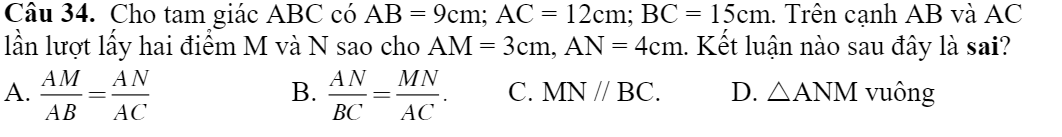\(\left(a+b+c+d\right)\left(a-b-c+d\right)=\left(a-b+c-d\right)\left(a+b-c-d\right)\\ \Rightarrow\dfrac{a+b+c+d}{a-b+c-d}=\dfrac{a+b-c-d}{a-b-c+d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a+b+c+d}{a-b+c-d}=\dfrac{a+b-c-d}{a-b-c+d}=\dfrac{a+b+c+d-a-b+c+d}{a-b+c-d-a+b+c-d}=\dfrac{2c+2d}{2c-2d}=\dfrac{c+d}{c-d}\)
\(\dfrac{a+b+c+d}{a-b+c-d}=\dfrac{a+b-c-d}{a-b-c+d}=\dfrac{a+b+c+d+a+b-c-d}{a-b+c-d+a-b-c+d}=\dfrac{2a+2b}{2a-2b}=\dfrac{a+b}{a-b}\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\Rightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a+b-a+b}{c+d-c+d}=\dfrac{2b}{2d}=\dfrac{b}{d}\\ \dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a+b+a-b}{c+d+c-d}=\dfrac{2a}{2c}=\dfrac{a}{c}\\ \Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)

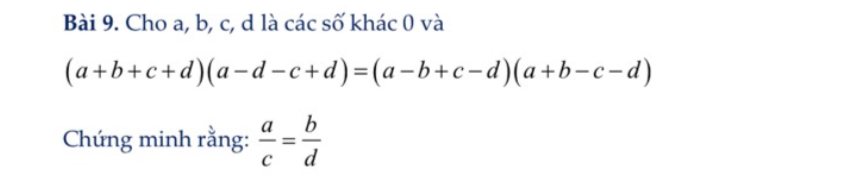



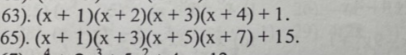

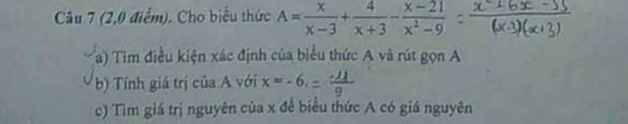

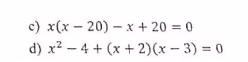 Mn giúp em 2 câu này với
Mn giúp em 2 câu này với
 giúp em 2 câu này vs ạ
giúp em 2 câu này vs ạ



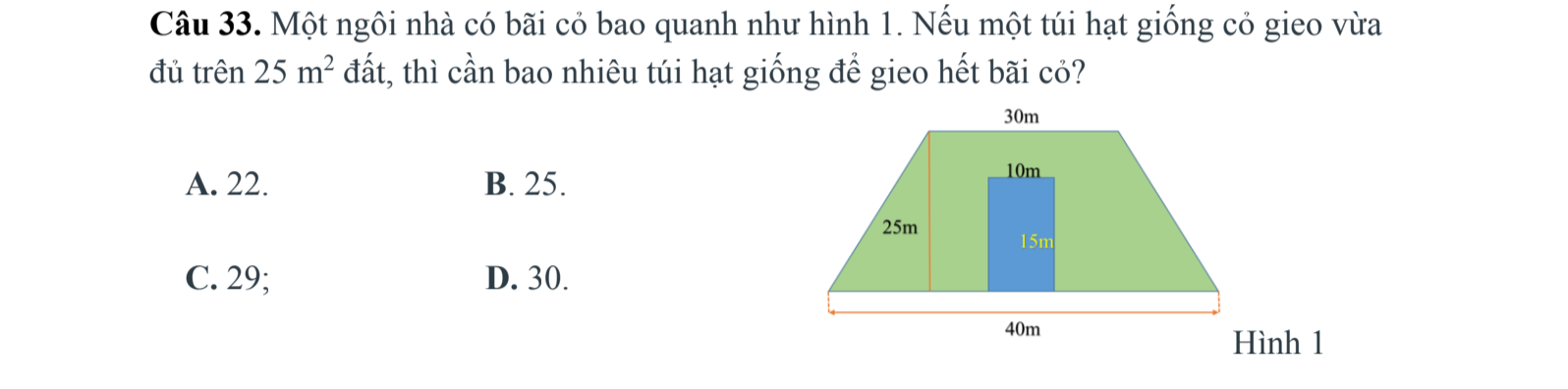
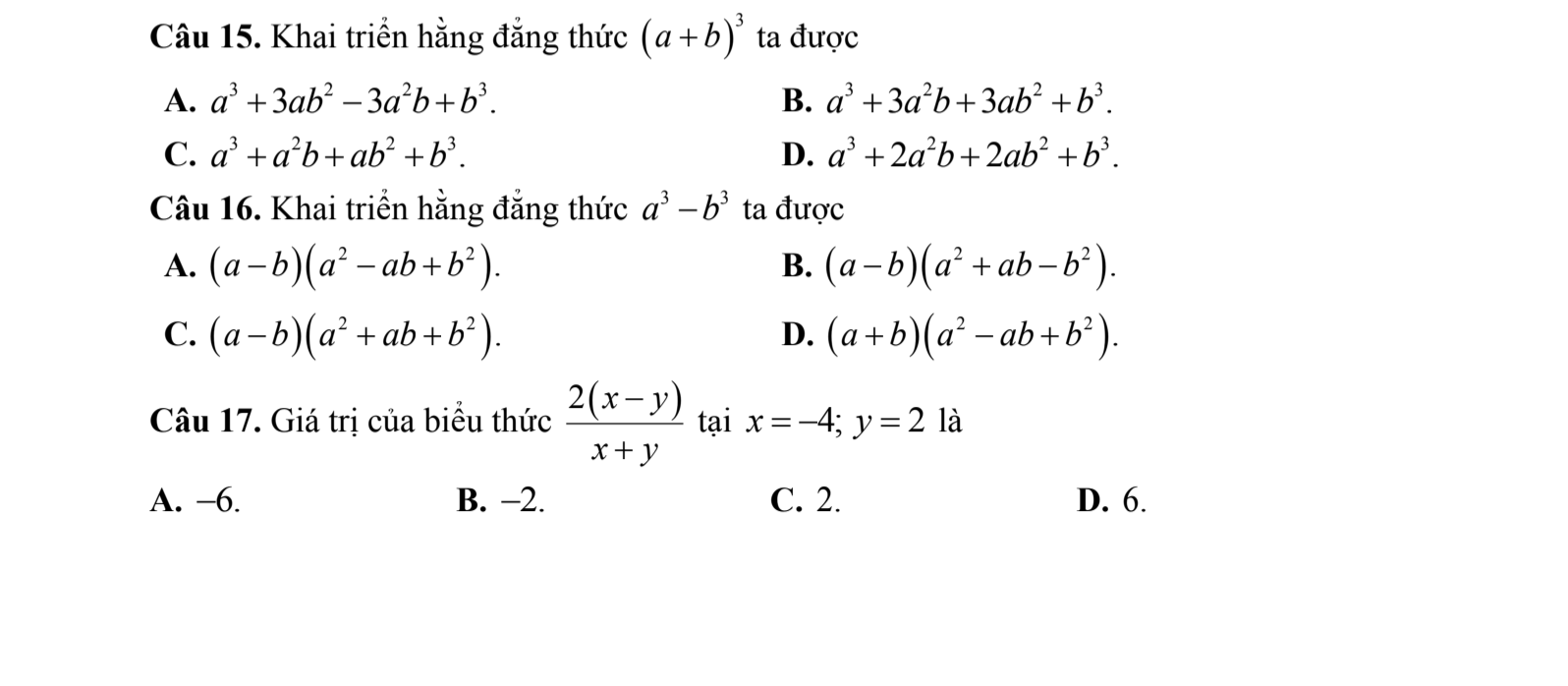


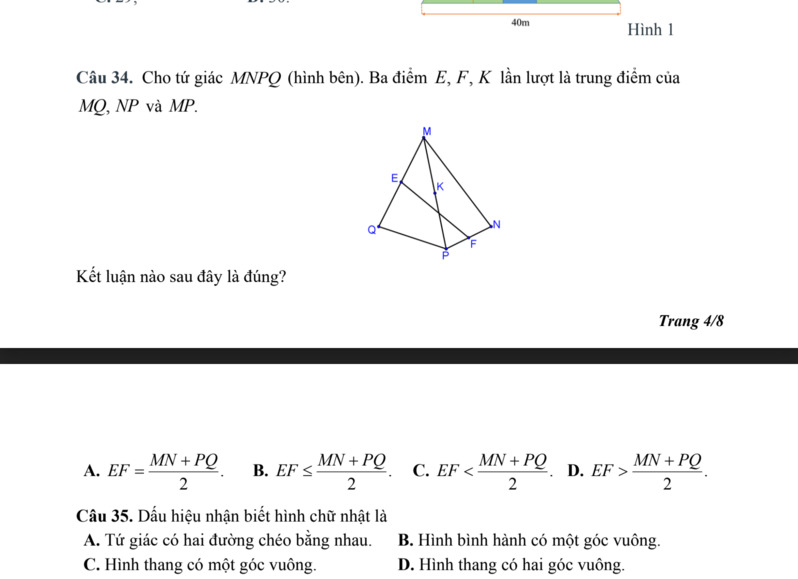

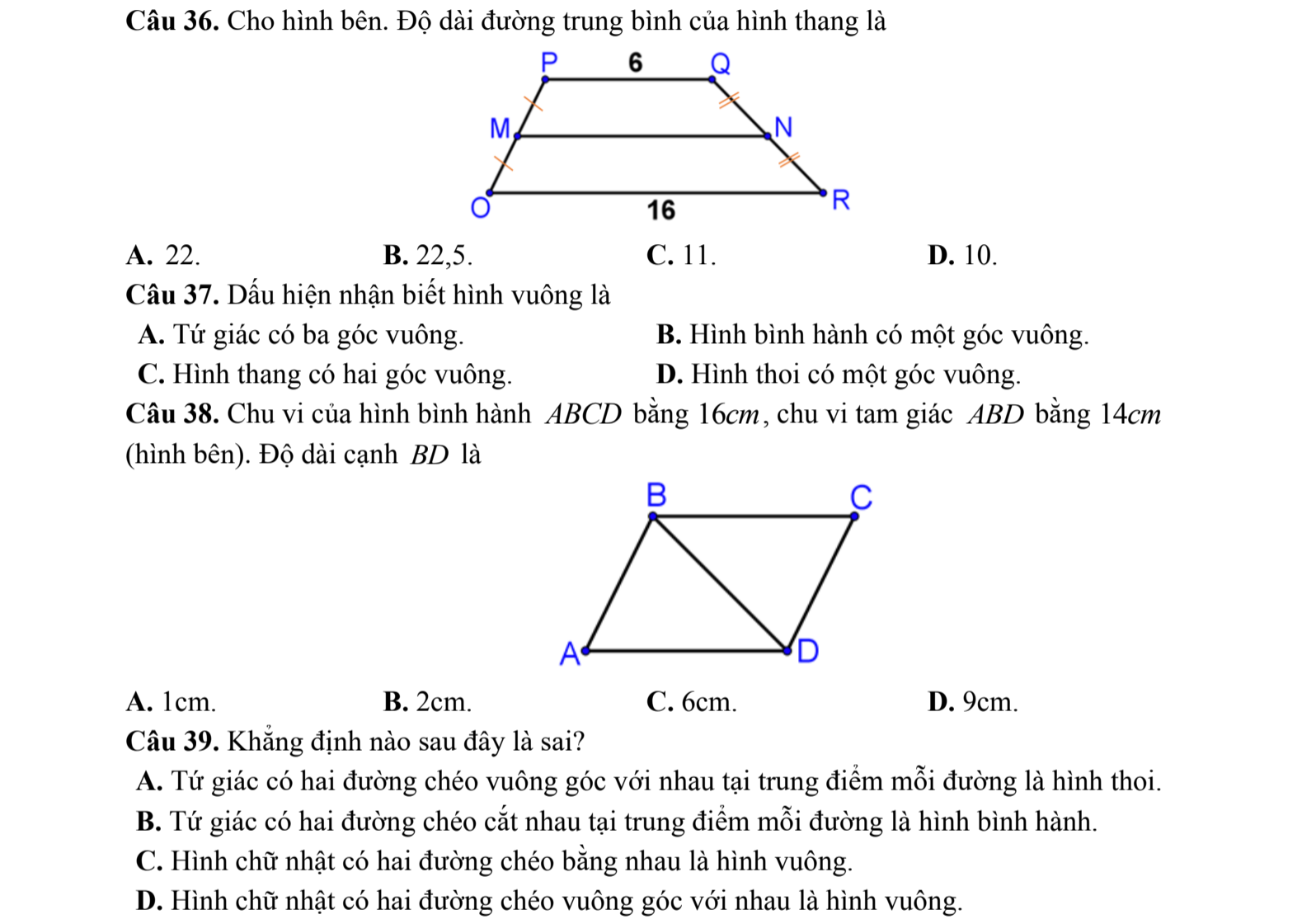


 Giúp em 45 câu trắc nghiệm này vs
Giúp em 45 câu trắc nghiệm này vs