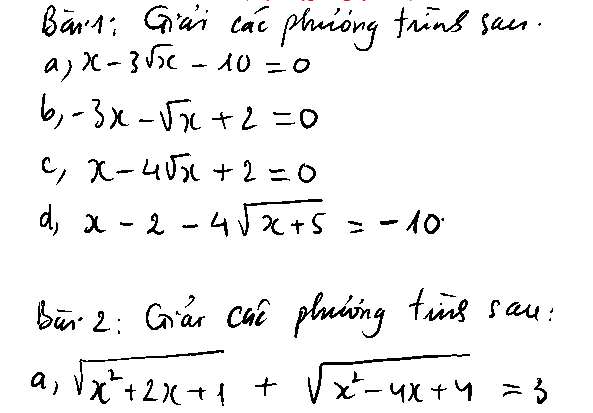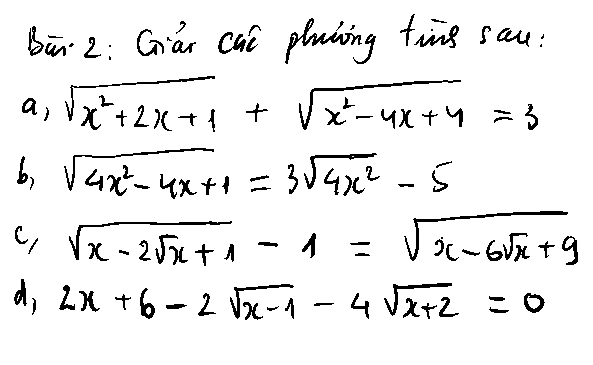1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
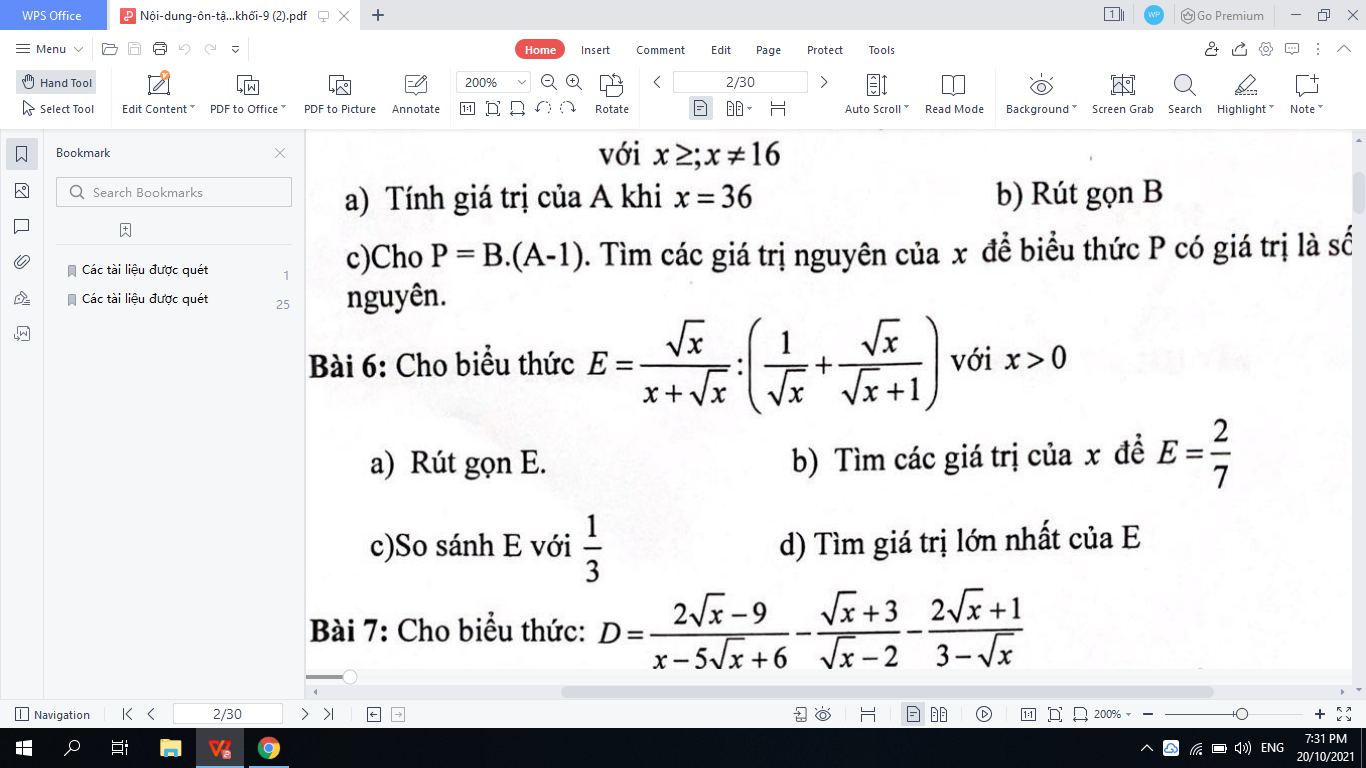
a)\(\left(\left(\sqrt{x}\right)^2-2\sqrt{x}\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{49}{4}=0\)
⇒\(\left(\sqrt{x}-\dfrac{3}{2}\right)^2=\dfrac{49}{4}\)
TH1:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{7}{2}\)⇒\(\sqrt{x}=5\)⇒x=25
TH2:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{-7}{2}\)⇒\(\sqrt{x}=-2\) vì \(\sqrt{x}\)≥0 loại
1.
a, ĐK: \(x\ge0\)
\(x-3\sqrt{x}-10=0\)
\(\Leftrightarrow x-5\sqrt{x}+2\sqrt{x}-10=0\)
\(\Leftrightarrow\left(\sqrt{x}-5\right)\left(\sqrt{x}+2\right)=0\)
\(\Leftrightarrow\sqrt{x}-5=0\)
\(\Leftrightarrow x=25\left(tm\right)\)
1.
b, ĐK: \(x\ge0\)
\(-3x-\sqrt{x}+2=0\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)\left(-3\sqrt{x}+2\right)=0\)
\(\Leftrightarrow-3\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}=\dfrac{2}{3}\)
\(\Leftrightarrow x=\dfrac{4}{9}\left(tm\right)\)
1.
c, ĐK: \(x\ge0\)
\(x-4\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}=2\pm\sqrt{2}\)
\(\Leftrightarrow x=6\pm4\sqrt{2}\left(tm\right)\)