\(\Delta=\left(2a-1\right)^2-4\left(-4a-3\right)=4a^2-12a+13=\left(2a-3\right)^2+4>0;\forall a\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm phân biệt với mọi a
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2a-1\\x_1x_2=-4a-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x_1+x_2\right)=4a-2\\x_1x_2=-4a-3\end{matrix}\right.\)
Cộng vế:
\(\Rightarrow2\left(x_1+x_2\right)+x_1x_2=-5\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc a

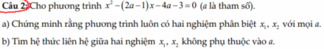




 Giúp em câu 2 với ạ. Em cảm ơn nhiều
Giúp em câu 2 với ạ. Em cảm ơn nhiều