4c.
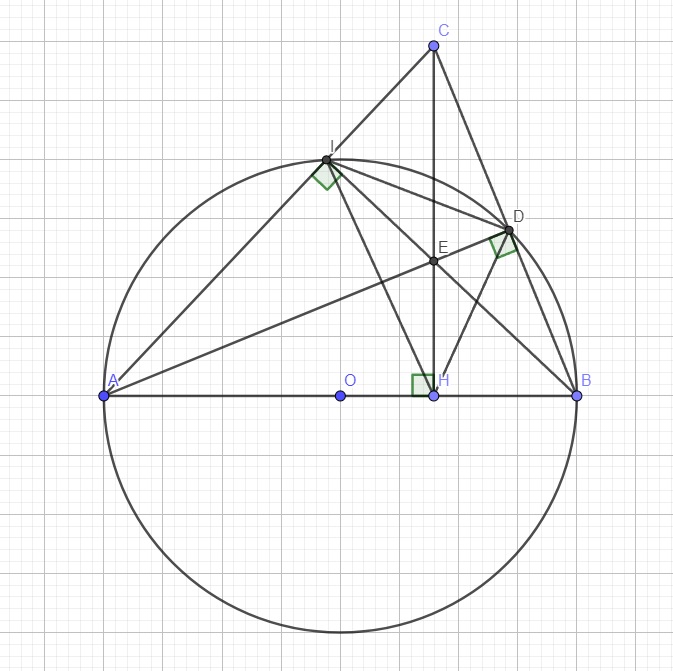
\(\widehat{CDE}=90^0\Rightarrow\) CE là đường kính của đường tròn ngoại tiếp CDE
Mà I thuộc đường tròn ngoại tiếp CDE \(\Rightarrow\widehat{CIE}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow EI\perp AC\) (1)
Do \(\left\{{}\begin{matrix}AD\perp BC\\CD\perp AB\end{matrix}\right.\) \(\Rightarrow E\) là giao điểm 2 đường cao của tam giác ABC
\(\Rightarrow E\) là trực tâm tam giác ABC (2)
(1);(2) \(\Rightarrow EI\) là đường cao thứ 3
\(\Rightarrow EI\) đi qua đỉnh B \(\Rightarrow B,I,E\) thẳng hàng
\(\Rightarrow\widehat{AIB}=90^0\Rightarrow I\) thuộc đường tròn đường kính AB
Hay I thuộc (O)
Theo cm câu a, BDEH nội tiếp \(\Rightarrow\widehat{EDH}=\widehat{EBH}\) (cùng chắn EH)
Hay \(\widehat{EDH}=\widehat{IBA}\)
Lại có A,B,I,D đều thuộc (O) nên ABID nội tiếp (O)
\(\Rightarrow\widehat{IBA}=\widehat{IDA}\) (cùng chắn IA)
\(\Rightarrow\widehat{EDH}=\widehat{IDA}\)
\(\Rightarrow DA\) là phân giác của \(\widehat{HDI}\)
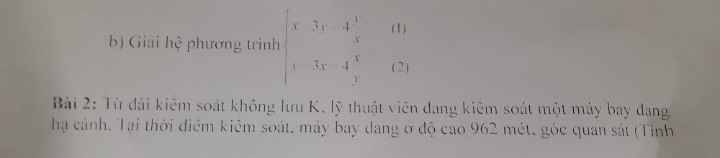
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
