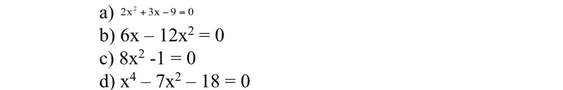\(a,2x^2+3x-9=0\\ \Leftrightarrow\left(2x^2+6x\right)-\left(3x+9\right)=0\\ \Leftrightarrow2x\left(x+3\right)-3\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(b,6x-12x^2=0\\ \Leftrightarrow6x\left(1-2x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(c,8x^2-1=0\\ \Leftrightarrow x^2=\dfrac{1}{8}\\ \Leftrightarrow x=\pm\dfrac{\sqrt{2}}{4}\)
\(d,x^4-7x^2-18=0\\ \Leftrightarrow\left(x^4-3x^3\right)+\left(3x^3-9x^2\right)+\left(2x^2-6x\right)+\left(6x-18\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^3+3x^2+2x+6\right)=0\\ \Leftrightarrow\left(x-3\right)\left[x^2\left(x+3\right)+2\left(x+3\right)\right]=0\\ \Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x^2+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x^2=-2\left(vô.lí\right)\end{matrix}\right.\)