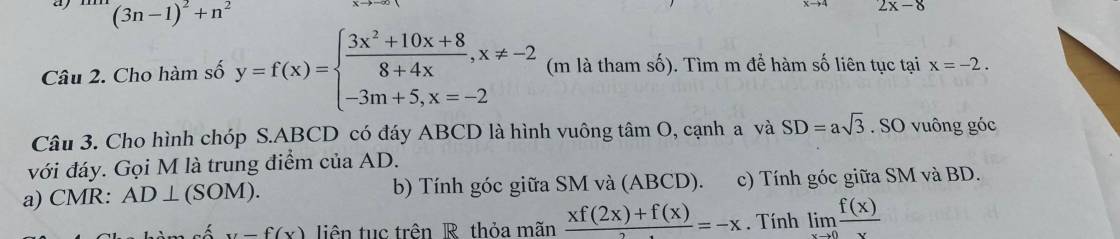b.
\(SO\perp\left(ABCD\right)\Rightarrow OM\) là hình chiếu vuông gốc của SM lên (ABCD)
\(\Rightarrow\widehat{SMO}\) là góc giữa SM và (ABCD)
\(BD=a\sqrt{2}\Rightarrow SO=\sqrt{SD^2-OD^2}=\sqrt{3a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{10}}{2}\)
\(OM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow tan\widehat{SMO}=\sqrt{10}\Rightarrow\widehat{SMO}=...\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(SM;BD\right)}=\widehat{\left(SM;MN\right)}=\widehat{SMN}\)
\(OM=ON\Rightarrow SN=SM=\sqrt{SO^2+OM^2}=\dfrac{a\sqrt{11}}{2}\)
Định lý hàm cos:
\(cos\widehat{SMN}=\dfrac{SM^2+MN^2-SN^2}{2SM.MN}=\dfrac{\sqrt{22}}{22}\Rightarrow\widehat{SMN}=...\)