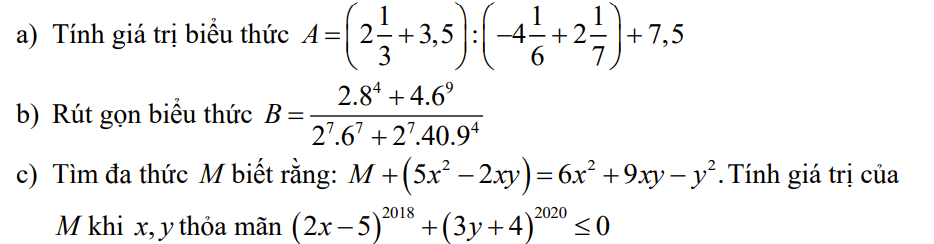`c)`
Ta có `(2x-5)^2018>=0AAx;(3y+4)^2020>=0AAy`
`=>(2x-5)^2018+(3y+4)^2020>=0AAx;y`
mà `(2x-5)^2018+(3y+4)^2020<=0`
`=>(2x-5)^2018+(3y+4)^2=0`
`<=>{(2x-5=0),(3y+4=0):}`
`<=>{(x=5/2),(y=-4/3):}`
Ta có:`M+(5x^2-2xy)=6x^2+9xy-y^2`
`=>M=6x^2+9xy-y^2-5x^2+2xy`
`=>M=x^2 +11xy-y^2`
Thay `x=5/2;y=-4/3`
`M=(5/2)^2 +11 . 5/2 . (-4/3)-(-4/3)^2`
`=-1159/36`
`M+(5x^2 -2xy)=6x^2 +9xy -y^2`
`=> M=6x^2+9xy-y^2-(5x^2 -2xy)`
`=> M=6x^2+9xy-y^2-5x^2 +2xy`
`=> M=x^2+11xy-y^2`
Ta có:
\(\left(2x-5\right)^{2018}\ge0\forall x;\left(3y+4\right)^{2020}\ge0\forall y\\
\Rightarrow\left(2x-5\right)^{2018}+\left(3y+4\right)^{2020}\ge0\forall x,y\)
Mà đề cho `(2x-5)^2018 + (3y+4)^2020 <= 0`
`=> `(2x-5)^2018 + (3y+4)^2020 =0`
Dấu "=" xảy ra `<=> {(2x-5=0),(3y+4=0):} <=> {(x= 5/2),(y = -4/3):}`
Thay `x= 5/2 ; y = -4/3` vào `M` ta có:
\(M=6x^2+11xy-y^2\\
=6.\left(\dfrac{5}{2}\right)^2+11.\dfrac{5}{2}.\dfrac{-4}{3}-\left(-\dfrac{4}{3}\right)^2\\
=6.\dfrac{25}{4}-\dfrac{110}{3}-\dfrac{16}{9}\\
=\dfrac{75}{2}-\dfrac{346}{9}\\
=-\dfrac{17}{18}\)