Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với ![]()
⇒ ![]()
⇒ ![]()
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
![]()
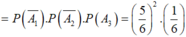
Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với ![]()
⇒ ![]()
⇒ ![]()
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
![]()
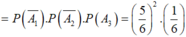
Gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp. Tính xác suất để 1) lần thứ nhất được số chấm chẵn và lần thứ hai được số chấm lẻ. 2) hai lần gieo có số chấm như nhau. 3) mặt 6 chấm xuất hiện ít nhất một lần. 4) tổng số chấm xuất hiện trong hai lần gieo bé hơn 10.
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số a b c ¯ chia hết cho 45” là
A . 1 216
B . 1 54
C . 1 72
D . 1 108
Kết quả (b;c) của việc gieo con súc sắc cân đối và đồng chất hai lần (trong đó b là số chấm xuất hiện trong lần gieo đầu, c là số chấm xuất hiện ở lần gieo thứ hai) được thay vào phương trình x 2 + b x + c x + 1 = 0 (*). Xác suất để phương trình (*) vô nghiệm là :
A. 17 36
B. 1 2
C. 1 6
D. 19 36
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn chấm?
A . 1 6
B . 1 4
C . 1 2
D . 1 3
Kết quả (b,c) của việc gieo con súc sắc cân đối và đồng chất hai lần, trong đó blà số chấm xuất hiện trong lần gieo đầu, clà số chấm xuất hiện ở lần gieo thứ hai, được thay vào phương trình bậc hai x2 + bx + c = 0. Tính xác suất để phương trình có nghiệm.
A. 19 36
B. 1 18
C. 1 2
D. 17 36
Kết quả (b,c) của việc gieo một con súc sắc cân đối hai lần liên tiếp, trong đó b là số chấm xuất hiện lần gieo thứ nhất, c là số chấm xuất hiện lần gieo thứ hai được thay vào phương trình bậc hai được thay vào phương trình bậc hai x 2 + bx + c = 0 . Tính xác suất để phương trình bậc hai đó vô nghiệm.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Kết quả (b,c) của việc gieo con súc sắc cân đối và đồng chất hai lần, trong đó b là số chấm suất hiện trong lần gieo đầu, c là số chấm suất hiện ở lần gieo thứ hai, được thay vào phương trình bậc hai ![]() . Tính xác suất để phương trình có nghiệm
. Tính xác suất để phương trình có nghiệm
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Kết quả (b,c)của việc gieo con súc sắc cân đối và đồng chất hai lần, trong đó b là số chấm xuất hiện trong lần gieo đầu, c là số chấm xuất hiện ở lần gieo thứ hai, được thay vào phương trình bậc hai x 2 + b x + c = 0
Tính xác suất để
a) Phương trình vô nghiệm;
b) Phương trình có nghiệm kép;
c) Phương trình có nghiệm.
Kết quả (b,c) của việc gieo một con súc sắc cần đối hai lần liên tiếp, trong đó b là số chấm xuất hiện trong lần gieo thứ nhất, c là số chấm xuất hiện trong lần gieo thứ hai được thay vào phương trình bậc hai x 2 + bx + c = 0 (x ∈ ℝ ). Tính xác suất để phương trình bậc hai đó có nghiệm.
A . 5 12
B . 13 36
C . 19 36
D . 31 36