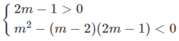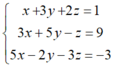Đặt `{(sqrt (x-2) = a), (sqrt (x+2) = b):}`
`-> ab = sqrt(x^2 - 4)`.
Ptr trở thành:
`a - b = 2ab - (a^2 + b^2) + 2`
`a - b + a^2 + b^2 - 2ab - 2 =0`
`<=> (a-b)^2 + (a-b) - 2 = 0`
Đặt `a - b = t`.
`-> t^2 + t - 2 = 0`
`<=> (t-1)(t+2) = 0`
`->` \(\left[{}\begin{matrix}t=1\\t=-2\end{matrix}\right.\)
`+, t = 1 -> a - b = 1 -> sqrt(x-2) - sqrt(x+2) = 1`
`-> sqrt(x-2) = 1 + sqrt(x+2)`
`-> x - 2 = 3 + x + 2sqrt(x+2)`
`-> sqrt(x+2) = -2,5`
`-> x = cancel O`.
`+, t = -2 -> sqrt(x-2) - sqrt(x+2) = -2`
`<=> sqrt(x-2) + 2 = sqrt(x+2)`
`<=> x + 2 + 4sqrt(x-2) = x + 2`
`<=> 4 sqrt(x-2) = 0`
`<=> sqrt(x-2) = 0`
`<=> x = 2`.
Vậy pt có một nghiệm duy nhất là `2`