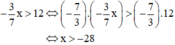\(\left(2x+3\right)^3+\left(3x-5\right)^3=\left(5x-2\right)^3-\left(5x-2\right)\left(17x^2+2016x-2063\right)\)
\(\Leftrightarrow\left\{\left(2x+3\right)^3+\left(3x-5\right)^3+3\left(2x+3\right)\left(3x-5\right)\left[\left(2x+3\right)+\left(3x-5\right)\right]\right\}-3\left(2x+3\right)\left(3x-5\right)\left[\left(2x+3\right)+\left(3x-5\right)\right]=\left(5x-2\right)^3-\left(5x-2\right)\left(17x^2+2016x-2063\right)\)
\(\Leftrightarrow\left(2x+3+3x-5\right)^3-3\left(2x+3\right)\left(3x-5\right)\left(2x+3+3x-5\right)=\left(5x-2\right)^3-\left(5x-2\right)\left(17x^2+2016x-2063\right)\)
\(\Leftrightarrow\left(5x-2\right)^3-3\left(5x-2\right)\left(2x+3\right)\left(3x-5\right)=\left(5x-2\right)^3-\left(5x-2\right)\left(17x^2+2016x-2063\right)\)
\(\Leftrightarrow3\left(5x-2\right)\left(2x+3\right)\left(3x-5\right)-\left(5x-2\right)\left(17x^2+2016x-2063\right)=0\)
\(\Leftrightarrow\left(5x-2\right)\left[3\left(2x+3\right)\left(3x-5\right)-\left(17x^2+2016x-2063\right)\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=0\\3\left(2x+3\right)\left(3x-5\right)-\left(17x^2+2016x-2063\right)=0\end{matrix}\right.\)
Trường hợp 1: \(5x-2=0\Leftrightarrow x=\dfrac{2}{5}\)
Trường hợp 2: \(3\left(2x+3\right)\left(3x-5\right)-\left(17x^2+2016x-2063\right)=0\)
\(\Leftrightarrow3\left(6x^2-10x+9x-15\right)-\left(17x^2+2016x-2063\right)=0\)
\(\Leftrightarrow18x^2-30x+27x-45-17x^2-2016x+2063=0\)
\(\Leftrightarrow x^2-2019x+2018=0\)
\(\Leftrightarrow\left(x^2-2018x\right)-\left(x-2018\right)=0\)
\(\Leftrightarrow x\left(x-2018\right)-\left(x-2018\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2018\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2018=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2018\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{\dfrac{2}{5};1;2018\right\}.\)





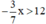 . Ta có:
. Ta có: