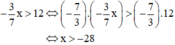\(\left(2x^2+x-2020\right)^2+4\left(x^2-5x-2021\right)^2=4\left(2x^2+x-2020\right)\left(x^2-5x-2021\right)\)
Đặt \(\left\{{}\begin{matrix}a=2x^2+x-2020\\b=x^2-5x-2021\end{matrix}\right.,\) khi đó phương trình trở thành:
\(a^2+4b^2=4ab\Leftrightarrow a^2-2.a.2b+\left(2b\right)^2=0\Leftrightarrow\left(a-2b\right)^2=0\Leftrightarrow a-2b=0\Leftrightarrow a=2b\)
Với \(a=2b,\) ta có:
\(2x^2+x-2020=2\left(x^2-5x-2021\right)\Leftrightarrow2x^2+x-2020=2x^2-10x-4042\Leftrightarrow11x=-2022\Leftrightarrow x=-\dfrac{2022}{11}\)
Vậy phương trình có tập nghiệm là: \(S=\left\{-\dfrac{2022}{11}\right\}.\)





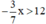 . Ta có:
. Ta có: