a) Ta có: \(OD=OE=DE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow\angle DOE\) đều \(\Rightarrow\) sđ \(\stackrel\frown{DE}=60\)
Ta có: \(\angle ACB=\dfrac{1}{2}sđ\left(\stackrel\frown{AB}-\stackrel\frown{DE}\right)=\dfrac{1}{2}\left(180-60\right)=60\)
b) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle AEB=90\)
\(\Rightarrow\angle CDH+\angle CEH=90+90=180\Rightarrow CDHE\) nội tiếp
c) Vì \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot CB\end{matrix}\right.\Rightarrow H\) là trực tâm \(\Delta ACB\Rightarrow CH\bot AB\)









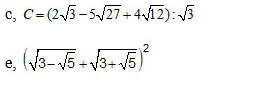
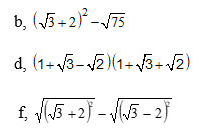 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp
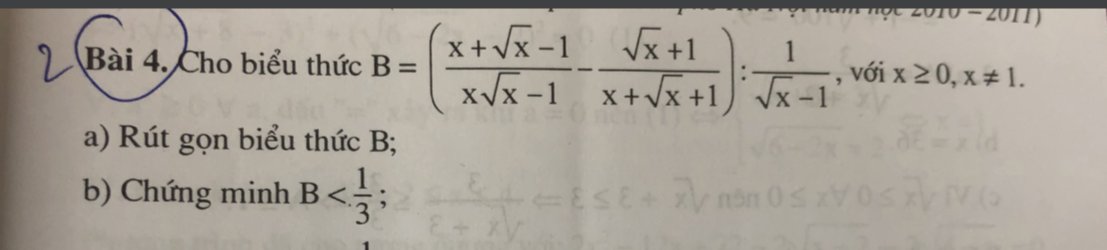


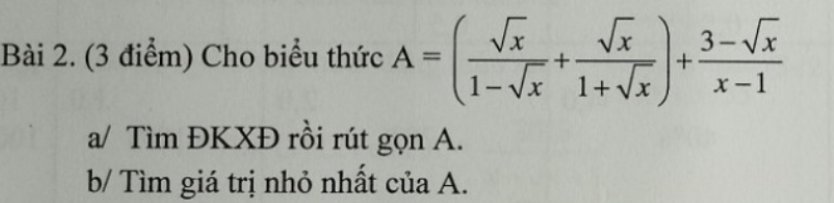

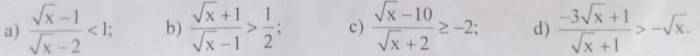 giải câu c và d hộ mik vs
giải câu c và d hộ mik vs 



