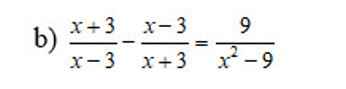\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)
Mn ơi giải câu này giúp mình vs ;-;;; Cảm ơn mn ạ
mn giúp mk vs : giải PT
2x^3 - 3x^2 - 5 = 0
Giải giúp pt này vs:
x(x+2)(x^2+2x+2)+1=0
ae giúp mình giải pt này vs cần gấp:
2014/2015+2015/2016+2016/2017
giúp e vs mn :( giải pt
6x4-x3-7x2+x+1=0
giải pt này giúp mình với nha mn....^_^ :
\(\left(x^2+x\right)^2+4\left(x^2+x\right)-12=0\)
\(8(x+\dfrac{1}{x} )^{2} \)\(+4(x^{2}+\dfrac{1}{x^{2} } )^{2}\)\(-4 (x^{2}+\dfrac{1}{x^{2}} )(x+\dfrac{1}{x})^{2} \)\(=(x+4)^{2}\)
giúp mik vs ạ cho mik cách giải pt này vs ạ
Giải pt :
(3x-2)(9x2+6x+4)-(3x-1)(9x2-3x+1)=x-4
9(2x+1)=4(x-5)2
MN giúp mk vs ! Sắp nộp r o(╥﹏╥)o
Mn ơi mn giúp mk bài này vs ạ. Thanks mn.
