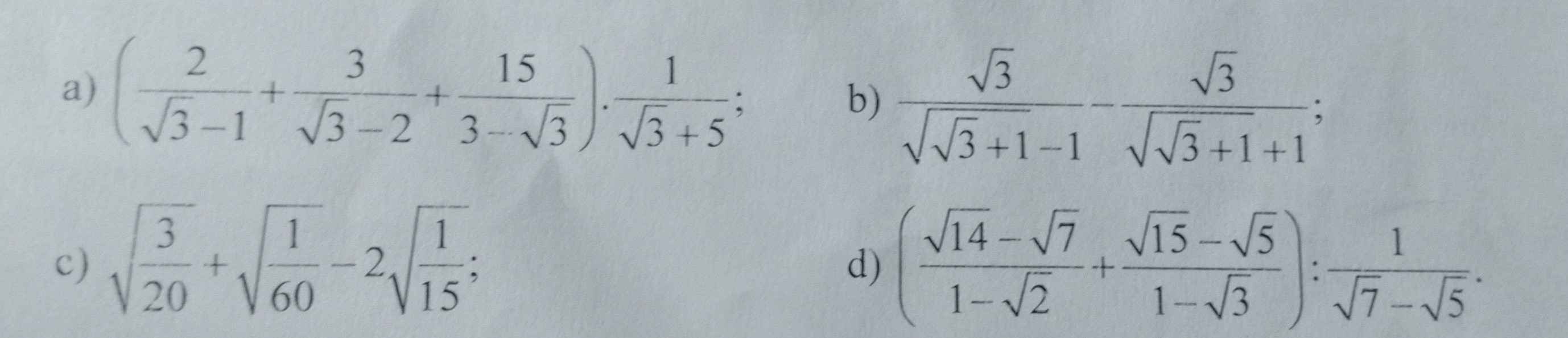Question

Giải giúp mình vs

Answer 1

Ta có \(\Delta ABC\) có các đường cao $BD;CE$

nên \(\widehat{BDC}=\widehat{CEB}=90^o\)  

suy ra $D;E$ cùng nhìn $[BC]$ dưới 1 góc không đổi

$D;E$ là 2 đỉnh liên tiếp tứ giác $BEDC$
suy ra tứ giác $BEDC$ nội tiếp (Bài toán quỹ tích cung chứa góc)

b, Xét $(O)$ có: $\widehat{xAC}=\widehat{ABC}$ (góc tạo bởi tia tiếp tuyến và dây cùng và góc nội tiếp cùng chắn cung $AC$)

hay $\widehat{xAC}=\widehat{EBC}$ 

Tứ giác $BEDC$ nội tiếp \(\Rightarrow\widehat{ADE}=\widehat{EBC}\)(góc ngoài tại 1 đỉnh = góc trong đỉnh đối diện)

suy ra  $\widehat{xAC}=\widehat{ADE}$

hay $\widehat{xAD}=\widehat{ADE}$

tức $xy//ED(đpcm)$

c, Tứ giác $BEDC$ nội tiếp \(\Rightarrow\widehat{EBD}=\widehat{ECD}\)(các góc nội tiếp cùng chắn cung $ED$) (đpcm)