\(A^2=8+2\sqrt{16-10-2\sqrt{5}}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{5}+1\)
Đặt \(\sqrt{10+2\sqrt5}\)= a. Ta có A = \(\sqrt{4+a}+\sqrt{4-a}\)
=> A2 = 4 + a + 4 - a + 2\(\sqrt{(4+a)(4-a)}\)
=> A2 = 8 + 2\(\sqrt{16-a^2}\)
=> A2 = 8 + 2\(\sqrt{16 - 10 + 2\sqrt5}\)
=> A2 = 8 + 2\(\sqrt{5+2\sqrt{5}+1}\)
=> A2 = 8 + 2\(\sqrt{(\sqrt{5}+1)^2}\)
=> A2 = 8 + 2\(\sqrt5\) + 2
=> A = \(\sqrt{2\sqrt{5}+10}\)
Ta có: \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\ge0\)
\(A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\)
\(=8+2\sqrt{16-10-2\sqrt{5}}=8+2\sqrt{6-2\sqrt{5}}\)
\(=8+2\sqrt{\left(\sqrt{5}-1\right)^2}=8+2\left(\sqrt{5}-1\right)=6+2\sqrt{5}\)
\(\Leftrightarrow A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)(do \(A\ge0\))

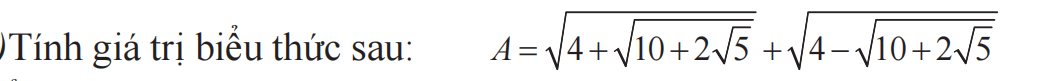












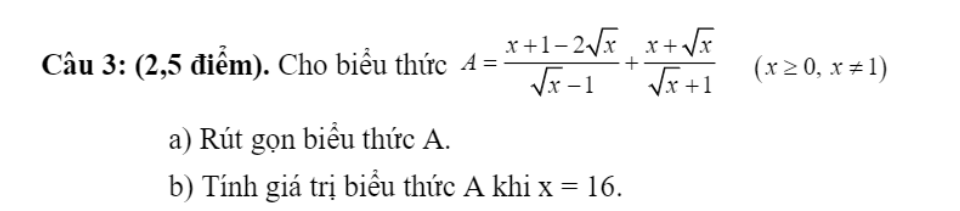

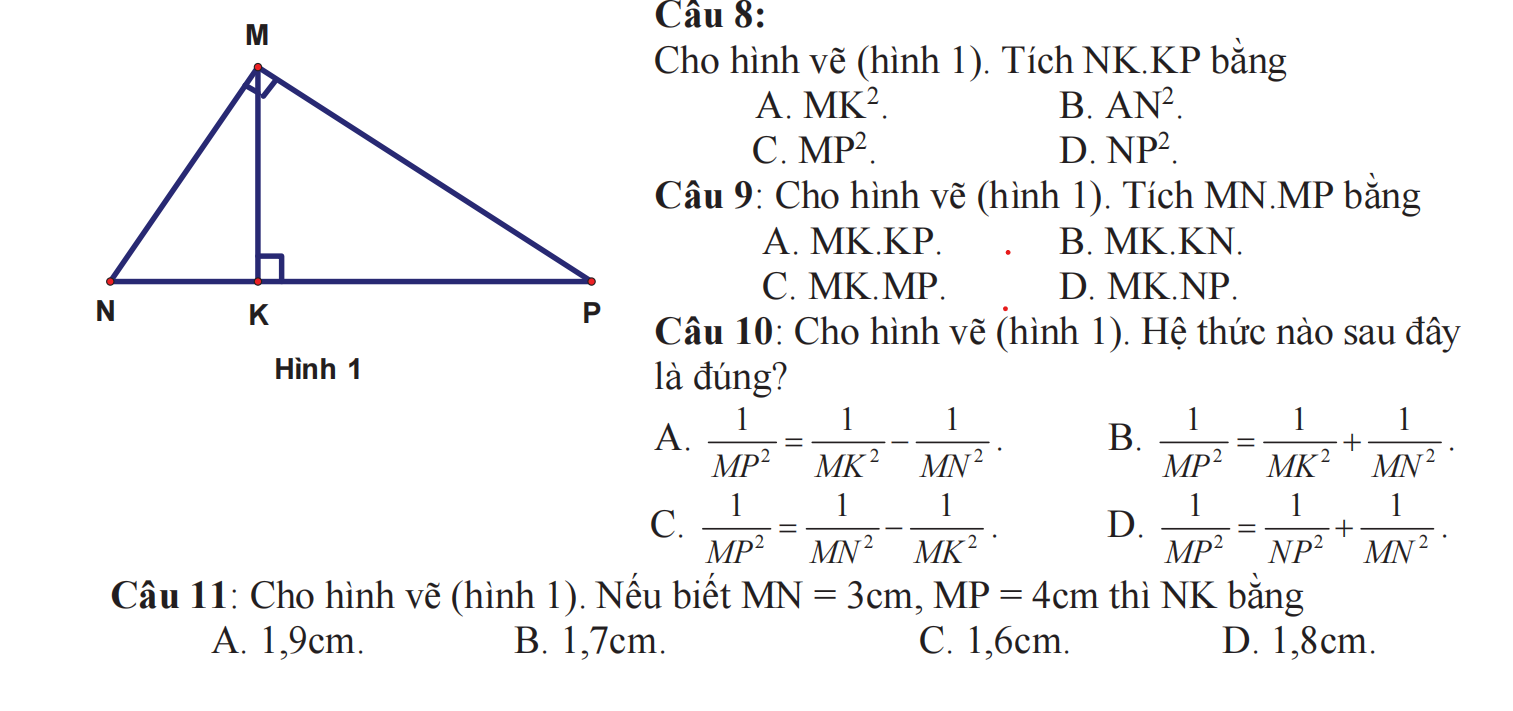

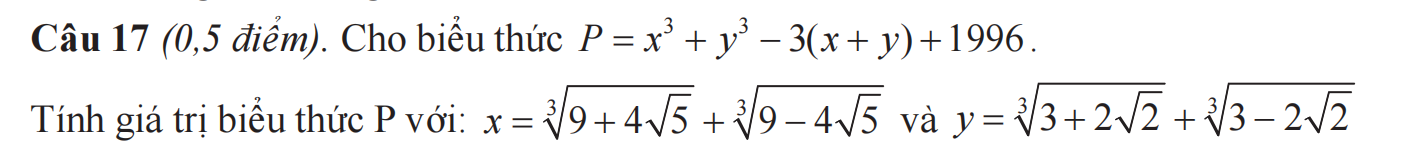 cảm ơn
cảm ơn 