\(\left(3x+1\right)\left(x-1\right)=0\)
\(\left[{}\begin{matrix}3x+1=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=1\end{matrix}\right.\)
\(e)3x(x-1)+x-1=0\\<=>3x(x-1)+(x-1)=0\\<=>(x-1)(3x+1)=0\\ <=>\left[\begin{matrix} x-1=0\\ 3x+1=0\end{matrix}\right.\\<=> \left[\begin{matrix} x=1\\ x=-1/3\end{matrix}\right.\)

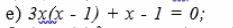










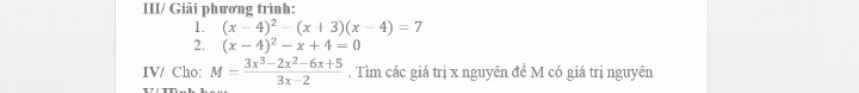

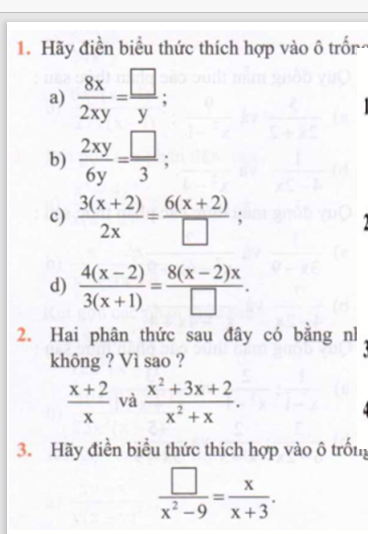 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ

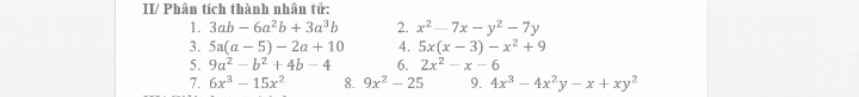


 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ