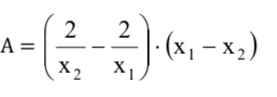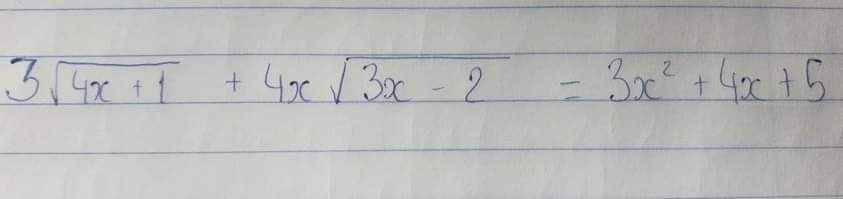Question

Giải giúp e ạ

Answer 1

\(1,A=\dfrac{5-3}{5+2}=\dfrac{2}{7}\\ 2,B=\dfrac{\sqrt{x}+2+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\\ 3,B\le\dfrac{3}{4}\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}-\dfrac{3}{4}\le0\\ \Leftrightarrow\dfrac{4\sqrt{x}+4-3\sqrt{x}-6}{4\left(\sqrt{x}+2\right)}\le0\\ \Leftrightarrow\sqrt{x}-2\le0\left(\sqrt{x}+2>0\right)\\ \Leftrightarrow\sqrt{x}\le2\\ \Leftrightarrow0< x< 4\left(x\ne4\right)\)

\(4,P=A:B=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\cdot\dfrac{ }{ }\)