\(ĐKXĐ:x\ge1\)
\(6x^2+5x+7=\sqrt{x^3-1}\)
\(\Leftrightarrow6x^2+5x+7=\sqrt{\left(x-1\right)\left(x^2+x+1\right)}\)
Đặt \(\left\{{}\begin{matrix}a=\sqrt{x-1}\\b=\sqrt{x^2+x+1}\end{matrix}\right.\). Từ phương trình trên ta có:
\(6b^2-a^2=ab\)
\(\Leftrightarrow\left(2b-a\right)\left(3b+a\right)=0\)
\(\Rightarrow2b=a\) (do \(a\ge0;b>0\) nên \(3b+a>0\))
\(\Rightarrow2\sqrt{x^2+x+1}=\sqrt{x-1}\)
\(\Leftrightarrow4x^2+4x+4=x-1\)
\(\Leftrightarrow4x^2+3x+5=0\).
Đến đây bấm máy ra phương trình vô nghiệm.
Vậy phương trình đã cho vô nghiệm.

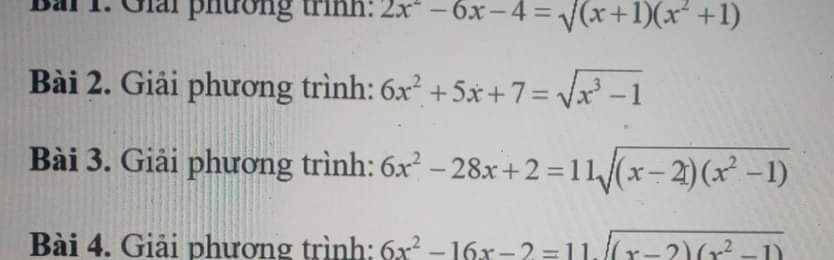







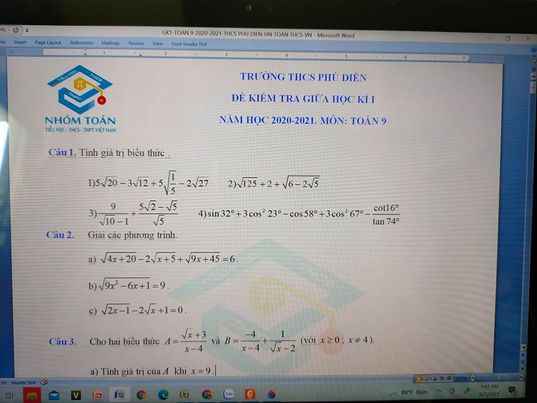 Giải giúp mình bài 1 bài 2 đi mn
Giải giúp mình bài 1 bài 2 đi mn







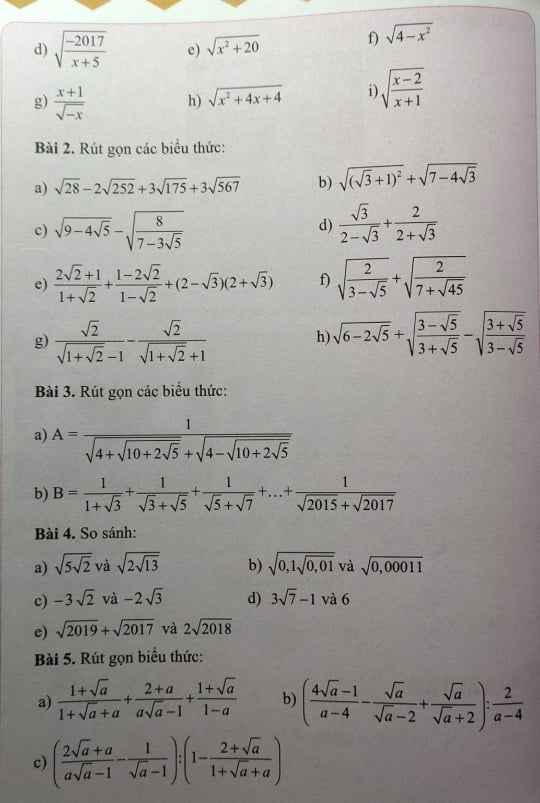 Giải giúp bài 2 nha
Giải giúp bài 2 nha