\(a)\left|x+\dfrac{1}{2}\right|=3\\ x+\dfrac{1}{2}=\left\{{}\begin{matrix}3\\-3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3-\dfrac{1}{2}\\-3-\dfrac{1}{2}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{5}{2}\\-\dfrac{7}{2}\end{matrix}\right.\)
\(b)\left|x-1,5\right|=2\\ x-1,5=\left\{{}\begin{matrix}2\\-2\end{matrix}\right.\\ x=\left\{{}\begin{matrix}2+1,5\\-2+1,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3,5\\-0,5\end{matrix}\right.\\ c)\left|x-2,5\right|-\dfrac{3}{4}=0\\ \left|x-2,5\right|=0+\dfrac{3}{4}\\ \left|x-2,5\right|=\dfrac{3}{4}\\ x-2,5=\left\{{}\begin{matrix}\dfrac{3}{4}\\-\dfrac{3}{4}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{3}{4}+2,5\\-\dfrac{3}{4}+2.5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3,25\\1,75\end{matrix}\right.\)
\(d)\dfrac{1}{2}-\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{3}\\ \left|\dfrac{5}{4}-2x\right|=\dfrac{1}{2}-\dfrac{1}{3}\\ \left|\dfrac{5}{4}-2x\right|=\dfrac{1}{6}\\ \dfrac{5}{4}-2x=\left\{{}\begin{matrix}\dfrac{1}{6}\\-\dfrac{1}{6}\end{matrix}\right.\\ 2x=\left\{{}\begin{matrix}\dfrac{5}{4}-\dfrac{1}{6}\\\dfrac{5}{4}-\left(-\dfrac{1}{6}\right)\end{matrix}\right.\\ 2x=\left\{{}\begin{matrix}\dfrac{13}{12}\\\dfrac{17}{12}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{12}:2\\\dfrac{17}{12}:2\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{24}\\\dfrac{17}{24}\end{matrix}\right.\)
\(e)\left|x-\dfrac{1}{2}\right|=4\\ x-\dfrac{1}{2}=\left\{{}\begin{matrix}4\\-4\end{matrix}\right.\\ x=\left\{{}\begin{matrix}4+\dfrac{1}{2}\\-4+\dfrac{1}{2}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{9}{2}\\-\dfrac{7}{2}\end{matrix}\right.\\ f)\left|x+2,5\right|=3\\ x+2,5=\left\{{}\begin{matrix}3\\-3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3-2,5\\-3-2,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}0,5\\-5,5\end{matrix}\right.\)
\(g)\left|x+1,5\right|-\dfrac{1}{4}=0\\ \left|x+1,5\right|=0+\dfrac{1}{4}\\ \left|x+1,5\right|=\dfrac{1}{4}\\ x-1,5=\left\{{}\begin{matrix}\dfrac{1}{4}\\-\dfrac{1}{4}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{1}{4}+1,5\\-\dfrac{1}{4}+1,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}1,75\\1,25\end{matrix}\right.\)
\(h)\dfrac{1}{5}-\left|\dfrac{1}{4}-3x\right|=\dfrac{1}{6}\\ \left|\dfrac{1}{4}-3x\right|=\dfrac{1}{5}-\dfrac{1}{6}\\ \left|\dfrac{1}{4}-3x\right|=\dfrac{1}{30}\\ \dfrac{1}{4}-3x=\left\{{}\begin{matrix}\dfrac{1}{30}\\-\dfrac{1}{30}\end{matrix}\right.\\ 3x=\left\{{}\begin{matrix}\dfrac{1}{4}-\dfrac{1}{30}\\\dfrac{1}{4}-\left(-\dfrac{1}{30}\right)\end{matrix}\right.\\ 3x=\left\{{}\begin{matrix}\dfrac{13}{60}\\\dfrac{17}{60}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{60}:3\\\dfrac{17}{60}:3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{180}\\\dfrac{17}{180}\end{matrix}\right.\)

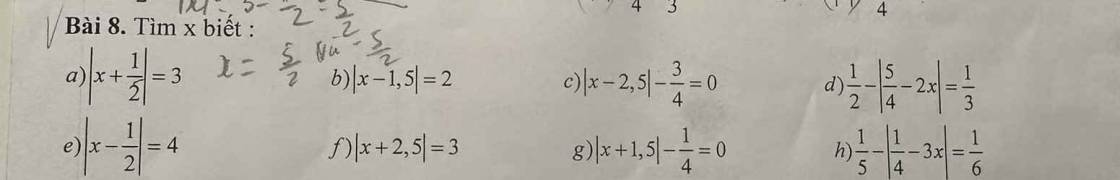



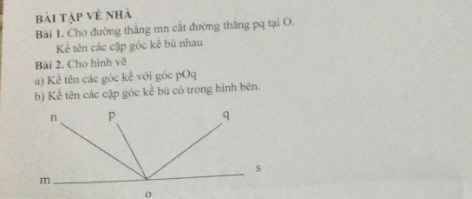
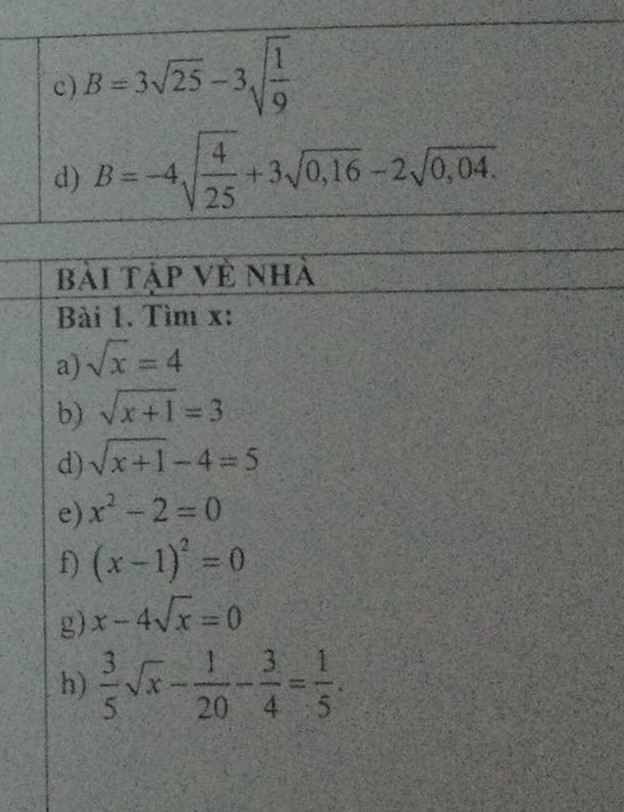
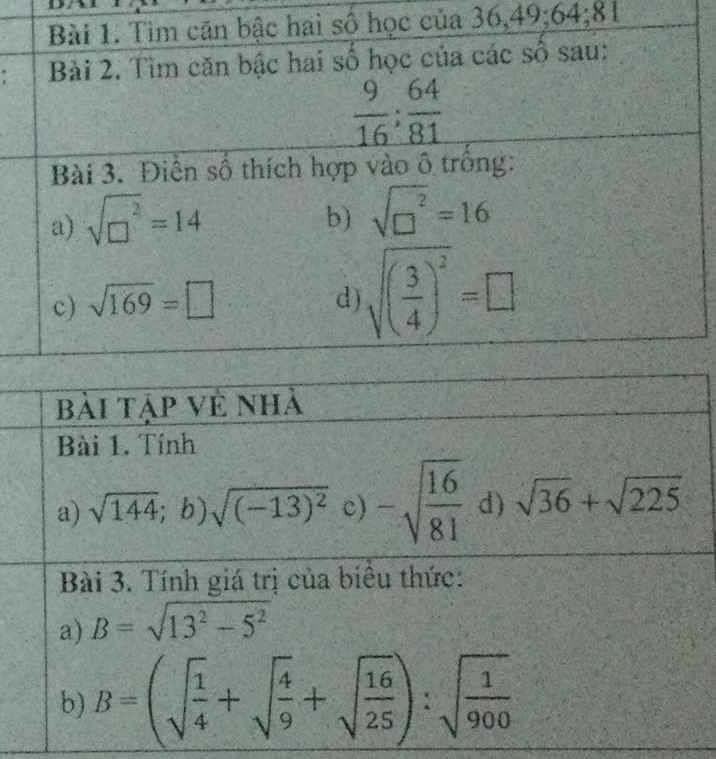
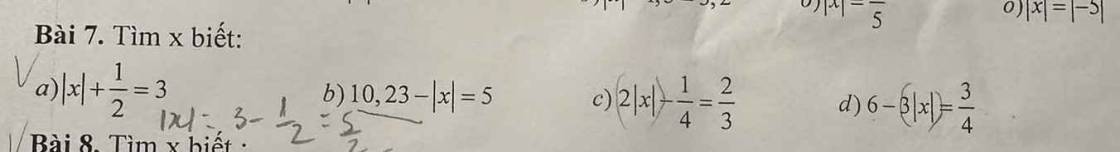
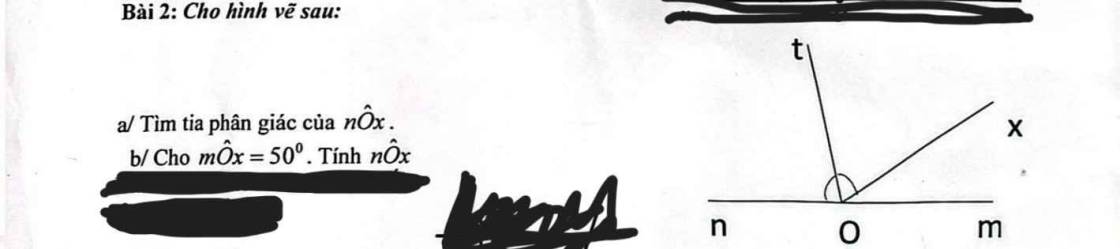

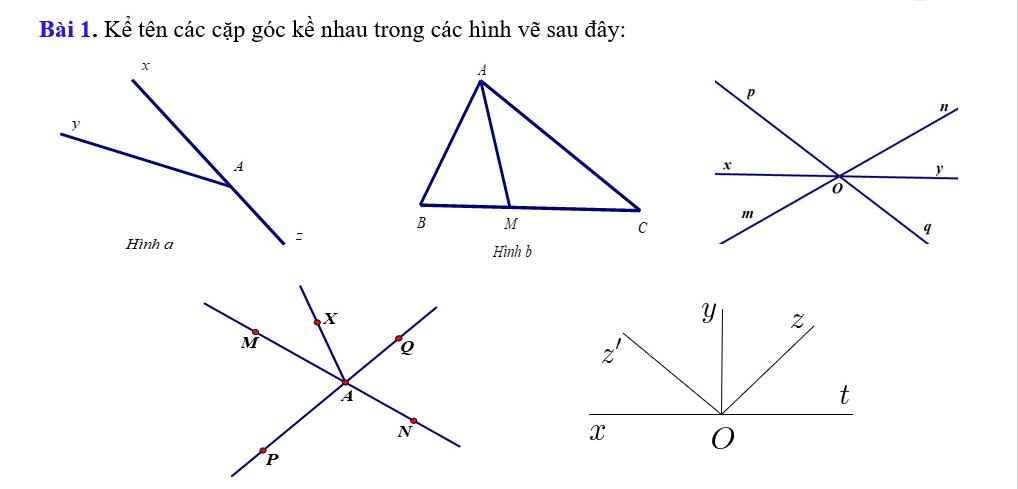 Giải gấp giúp t ạ
Giải gấp giúp t ạ
 T còn đúng 3 bài này th ạ, mg giải gấp giúp t với, 15p nx hạn nộp r
T còn đúng 3 bài này th ạ, mg giải gấp giúp t với, 15p nx hạn nộp r
 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ