a)\(MinA=1\Leftrightarrow x=\dfrac{1}{4}\)
b)\(MaxP=1\Leftrightarrow x=\dfrac{1}{4}\)
a) \(A=x-\sqrt{x}+\dfrac{5}{4}=\left(x-\sqrt{x}+\dfrac{1}{4}\right)+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+1\ge1\)
\(minA=1\Leftrightarrow x=\dfrac{1}{4}\)
b) \(P=\dfrac{1}{x-\sqrt{x}+\dfrac{5}{4}}=\dfrac{1}{\left(x-\sqrt{x}+\dfrac{1}{4}\right)+1}=\dfrac{1}{\left(\sqrt{x}-\dfrac{1}{2}\right)^2+1}\le\dfrac{1}{1}=1\)
\(maxP=1\Leftrightarrow x=\dfrac{1}{4}\)
a, \(A=x-\sqrt{x}+\dfrac{5}{4}\)
\(=x-\sqrt{x}+\dfrac{1}{4}+1\)
\(=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+1\ge1\)
\(\Rightarrow minA=1\Leftrightarrow x=\dfrac{1}{4}\)
b, \(P=\dfrac{1}{x-\sqrt{x}+\dfrac{5}{4}}=\dfrac{1}{A}\le\dfrac{1}{1}=1\)
\(\Rightarrow maxP=1\Leftrightarrow x=\dfrac{1}{4}\)









 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)



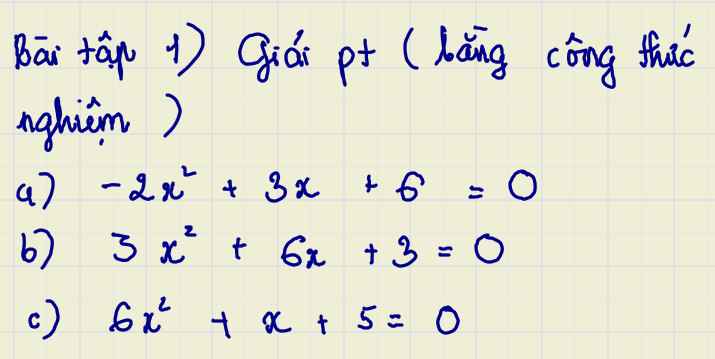

 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn



