Điều kiện:`a>=0,a ne 1` $\\$ `E=(1+(a-sqrta)/(sqrta-1))(1-(a+sqrta)/(1+sqrta))`
`=(1+(sqrta(sqrta-1))/(sqrta-1))(1-(sqrta(sqrta+1))/(sqrta+1))`
`=(1+sqrta)(1-sqrta)`
`=1-a`
\(E=\left(1+\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
ĐK: a ≥ 0; a khác 1
\(=\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)

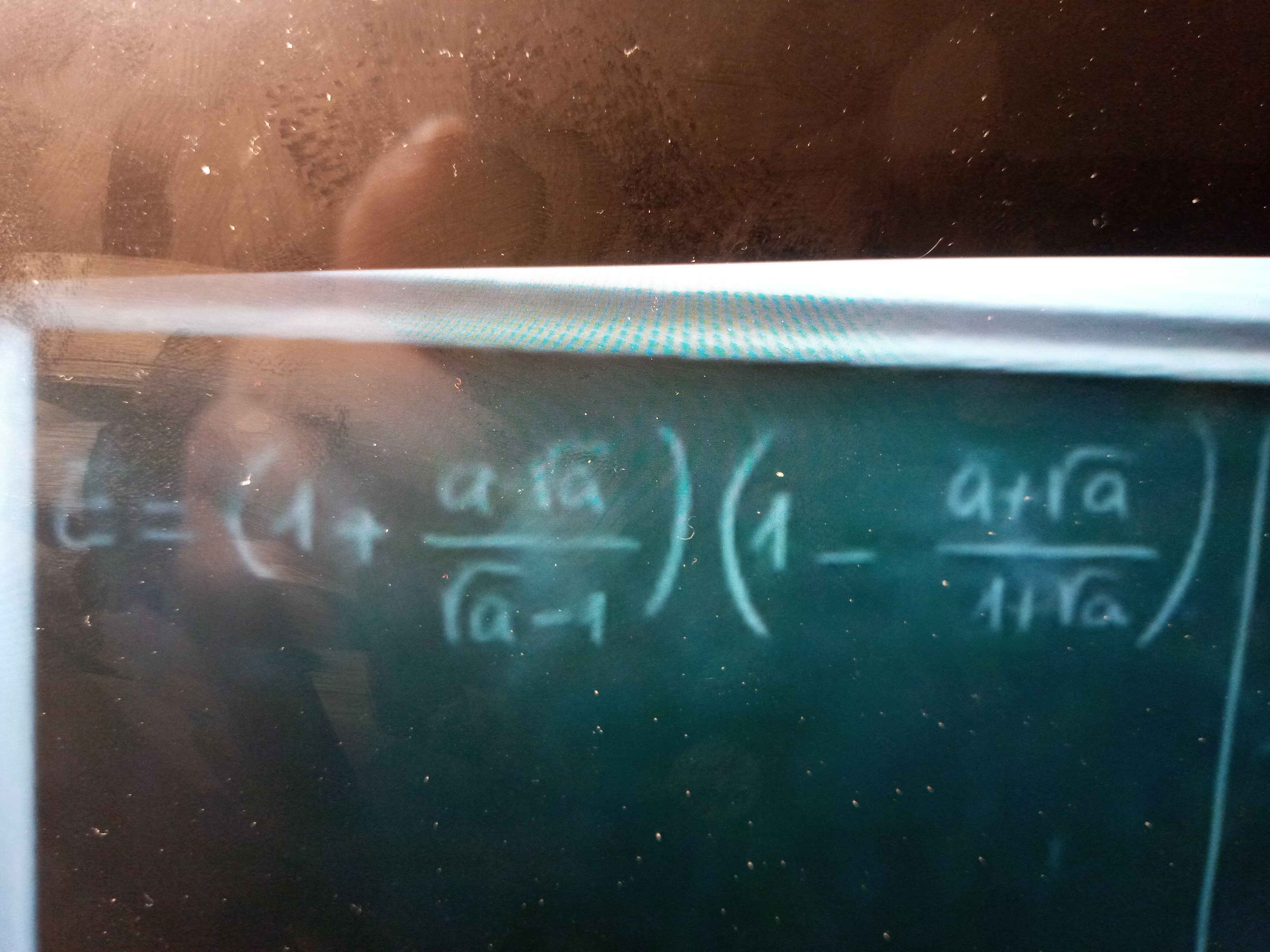






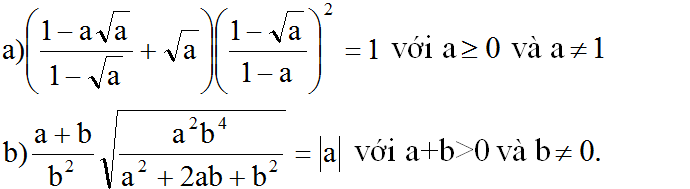





 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
