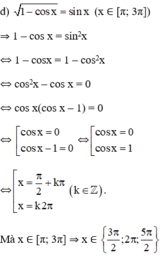
Thử lại: Trong 3 nghiệm trên thì nghiệm 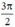 không thỏa mãn
không thỏa mãn
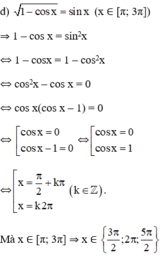
Thử lại: Trong 3 nghiệm trên thì nghiệm 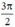 không thỏa mãn
không thỏa mãn
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Số nghiệm thuộc khoảng - 4 π 3 ; π 2 của phương trình cos ( π + x ) + 3 sin x = sin 3 x - 3 π 2 là
A. 6.
B. 2.
C. 4.
D. 3.
Số nghiệm thuộc khoảng [ - 4 π 3 ; π 2 ) của phương trình cos ( π + x ) + 3 sin x = sin 3 x - 3 π 2
A. 6.
B. 2.
C. 4.
D. 3.
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Giải giúp mình phương trình này với ạ
\(sin(x-{π\over6})^3+3sin(x+{π\over3})^3=cosx+sin2x\)
Tập nghiệm của phương trình sin(πx) = cos(π/3+πx) là
A. {π/12+kπ,k∈Z}
B. {1/12+k,k∈Z}
C. {π/2+kπ,k∈Z}
D. {1/2+kπ,k∈Z}
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Tìm tất cả các nghiệm của phương trình sin x + sin 2x + sin3x = 0 thuộc ( 0 ; π )
A. 3
B. 4
C. 5
D. 6
Phương trình sin ( 2 x - π 4 ) = sin ( x + 3 π 4 ) có tổng các nghiệm thuộc khoảng 0 , π bằng:
![]()
![]()
![]()
![]()