Ta có:
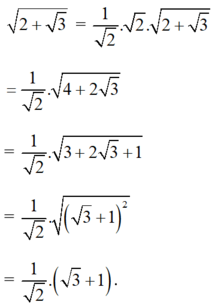
Giá trị biểu thức bằng:
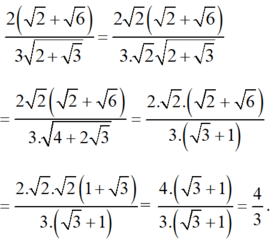
Chọn đáp án D.
Ta có:
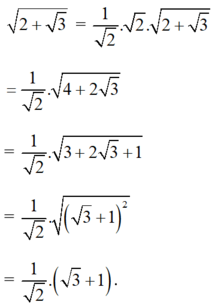
Giá trị biểu thức bằng:
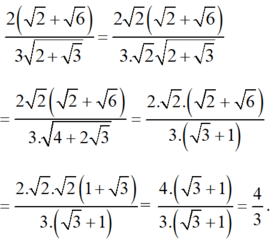
Chọn đáp án D.
Giá trị của biểu thức 2 ( 2 + 6 ) 3 2 + 3 bằng
A . 2 2 3 B ⋅ 2 3 3 C .1 D . 4 3
Hãy chọn câu trả lời đúng
Giá trị của biểu thức
1 2 + 3 + 1 2 − 3 bằng A. 1 2 ; B. 1 ; C.-4 ; D. 4
Hãy chọn câu trả lời đúng.
Giá trị của biểu thức 1 2 + 3 + 1 2 - 3 b ằ n g A . 1 2 ; B . 1 ; C . - 4 ; D . 4
Hãy chọn câu trả lời đúng.
Câu 1. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 2. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 3. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Hãy giải ba câu hỏi này
Câu 1. Chứng minh √7 là số vô tỉ.
Câu 2.
a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
Câu 4.
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|
Câu 9.
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
Câu 10. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Câu 11. Tìm các giá trị của x sao cho:
a) |2x – 3| = |1 – x|
b) x2 – 4x ≤ 5
c) 2x(2x – 1) ≤ 2x – 1.
Câu 12. Tìm các số a, b, c, d biết rằng: a2 + b2 + c2 + d2 = a(b + c + d)
Câu 13. Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 1 a) Tìm câu bậc hai của mỗi số sau : 81; 9 trên 16 b) Tìm x để biểu thức sau có nghĩa : 3 trên căn 2-7x Câu 2 b) (2√3-3√2)^2 +2√6 +3√24 Câu 3 b) Giải Phương Trình : √27x-18-6=√3x-2 Câu6 a) với a là góc nhọn, hãy rút biểu thức: sin^6 alpha + cos^6 alpha +3sin^2 alpha × cos^2 alpha Câu 8: từ đỉnh một tòa nhà cao 54m, người tra nhìn thấy 1 ôtô đang đỗ dưới 1 góc nghiêng xuống là 40°. Hỏi ôtô đang đỗ cách tòa nhà đó khoảng bao nhiêu mét?
Bài 1: tìm x. Biết
a. x^2 =49
b. √2x =6
c. 2√x =6
d. √x-1 < √7
Bài 2: tính giá trị của biểu thức
a. √0.04 +√0.16
b. 70.08 + 14√0.36
c. (11- 4√3) . ( 11+ 4√3 )
d. ( 2 - √3 ) . ( 2 +√3 )
Câu 40** : Giá trị biểu thức: sin210o + sin230o + sin280o + sin260o bằng:
A, 0; B. 1; C. 2; D. 3 .
Chứng minh √7 là số vô tỉ.
Câu 2.
a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
Câu 4.
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
Câu 5. Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
Câu 6. Cho a3 + b3 = 2. Tìm giá trị lớn nhất của biểu thức: N = a + b.
Câu 7. Cho a, b, c là các số dương. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 8. Tìm liên hệ giữa các số a và b biết rằng: |a + b| > |a - b|