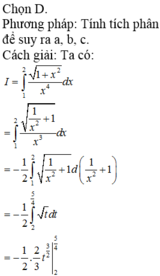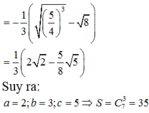Các câu hỏi tương tự
Trong không gian Oxyz cho mặt cầu
(
S
)
:
(
x
-
2
)
2
+
(
y
-
1
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 9 và điểm M ( a ; b ; c ) ∈ ( S ) sao cho biểu thức P=2a+2b+2c đạt giá trị nhỏ nhất. Tính T=a+b+c.
A. 2
B. 1
C. -2
D. -1
Biết
∫
x
+
1
(
x
-
1
)
(
x
-
2
)
d
x
a
ln
x
-
1
+
b
ln
x
-...
Đọc tiếp
Biết ∫ x + 1 ( x - 1 ) ( x - 2 ) d x = a ln x - 1 + b ln x - 2 + C , ( a , b ∈ ℝ ) . Tính giá trị của biểu thức
A. a+b =1
B. a+b =5
C. a+b =-5
D. a+b =-1
Gỉa sử \(\int\limits^5_3\dfrac{dx}{x^2-x}=aIn5+bIn3+cIn2\times\left(a,b,c\varepsilon Z\right)\) Tính giá trị biểu thức S\(-2a+b+3c^2\)
A. S= 3
B. S= 6
C. S= 0
D. S= -2
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho phương trình
2
log
4
2
x
2
-
x
+
2
m
-
4
m
2
+
log
1
2
x
2...
Đọc tiếp
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Biết
∫
0
1
3
x
-
1
(
x
+
3
)
2
d
x
ln
a
b
-
c
d
(
a
,
b
,...
Đọc tiếp
Biết ∫ 0 1 3 x - 1 ( x + 3 ) 2 d x = ln a b - c d ( a , b , c , d ∈ Z ) Giá trị của biểu thức a+b+c+d bằng
![]()
![]()
![]()
![]()
Tích phân
I
∫
0
1
(
x
-
1
)
2
x
2
+
1
d
x
a
ln
b
+
c
, trong đó a; b; c là số nguyên. Tính giá trị của biểu th...
Đọc tiếp
Tích phân I = ∫ 0 1 ( x - 1 ) 2 x 2 + 1 d x = a ln b + c , trong đó a; b; c là số nguyên. Tính giá trị của biểu thức a+b+c.
![]()
![]()
![]()
![]()
Tính giá trị bằng số của biểu thức 9 log 3 2
A. 2 B. 4
C. 1/3 D. 1/2
Tính giá trị bằng số của biểu thức 9 log 3 2
A. 2 B. 4
C. 1/3 D. 1/2