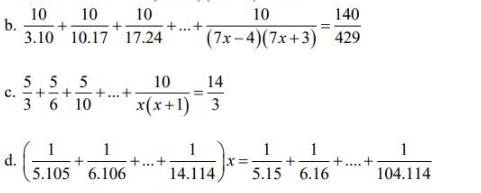b/
\(\frac{10}{3.10}+\frac{10}{10.17}+\frac{10}{17.24}+...+\frac{10}{(7x-4)(7x+3)}=\frac{140}{429}\\ \Rightarrow \frac{1}{3.10}+\frac{1}{10.17}+\frac{1}{17.24}+...+\frac{1}{(7x-4)(7x+3)}=\frac{14}{429}\)
\(\Rightarrow \frac{7}{3.10}+\frac{7}{10.17}+\frac{7}{17.24}+...+\frac{7}{(7x-4)(7x+3)}=\frac{98}{429}\\ \Rightarrow \frac{1}{3}-\frac{1}{10}+\frac{1}{10}-\frac{1}{17}+\frac{1}{17}-\frac{1}{24}+...+\frac{1}{7x-4}-\frac{1}{7x+3}=\frac{98}{429}\\ \Rightarrow \frac{1}{3}-\frac{1}{7x+3}=\frac{98}{429}\\ \Rightarrow \frac{1}{7x+3}=\frac{1}{3}-\frac{98}{429}=\frac{15}{143}\\ \Rightarrow 7x+3=\frac{143}{15}\Rightarrow x=\frac{14}{15}\)
d/
$\frac{1}{5.105}+\frac{1}{6.106}+...+\frac{1}{14.114}$
$=\frac{1}{100}\left(\frac{105-5}{5.105}+\frac{106-6}{6.106}+...+\frac{114-14}{14.114}\right)$
$=\frac{1}{100}\left(\frac{1}{5}-\frac{1}{105}+\frac{1}{6}-\frac{1}{106}+...+\frac{1}{14}-\frac{1}{114}\right)$
$=\frac{1}{100}\left[(\frac{1}{5}+\frac{1}{6}+...+\frac{1}{14})-(\frac{1}{105}+\frac{1}{106}+...+\frac{1}{114})\right](1)$
Lại có:
$\frac{1}{5.15}+\frac{1}{6.16}+...+\frac{1}{104.114}$
$=\frac{1}{10}\left(\frac{10}{5.15}+\frac{10}{6.16}+...+\frac{10}{104.114}\right)$
$=\frac{1}{10}\left(\frac{15-5}{5.15}+\frac{16-6}{6.16}+...+\frac{114-104}{104.114}\right)$
$=\frac{1}{10}\left(\frac{1}{5}-\frac{1}{15}+\frac{1}{6}-\frac{1}{16}+...+\frac{1}{104}-\frac{1}{114}\right)$
$=\frac{1}{10}\left[(\frac{1}{5}+\frac{1}{6}+...+\frac{1}{104})-(\frac{1}{15}+\frac{1}{16}+....+\frac{1}{114})\right]$
$=\frac{1}{10}\left[(\frac{1}{5}+\frac{1}{6}+...+\frac{1}{14})-(\frac{1}{105}+\frac{1}{106}+...+\frac{1}{114})\right](2)$
Từ $(1); (2)$ suy ra:
$\frac{1}{100}\left[(\frac{1}{5}+\frac{1}{6}+...+\frac{1}{14})-(\frac{1}{105}+\frac{1}{106}+...+\frac{1}{114})\right]x=\frac{1}{10}\left[(\frac{1}{5}+\frac{1}{6}+...+\frac{1}{14})-(\frac{1}{105}+\frac{1}{106}+...+\frac{1}{114})\right]$
$\Rightarrow x=10$
c/
$\frac{5}{3}+\frac{5}{6}+\frac{5}{10}+...+\frac{10}{x(x+1)}=\frac{14}{3}$
$\frac{10}{6}+\frac{10}{12}+\frac{10}{20}+...+\frac{10}{x(x+1)}=\frac{14}{3}$
$\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+....+\frac{1}{x(x+1)}=\frac{7}{15}$
$\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{x(x+1)}=\frac{7}{15}$
$\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+....+\frac{(x+1)-x}{x(x+1)}=\frac{7}{15}$
$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+....+\frac{1}{x}-\frac{1}{x+1}=\frac{7}{15}$
$\frac{1}{2}-\frac{1}{x+1}=\frac{7}{15}$
$\frac{1}{x+1}=\frac{1}{30}$
$\Rightarrow x+1=30$
$\Rightarrow x=29$.