1)Trong tam giác vuông BDC, cạnh huyền BC lớn hơn cạnh góc vuông BD.
Vậy BC > BD.
2)Chứng minh tương tự như trên, trong tam giác vuông CEB, cạnh huyền BC lớn hơn cạnh góc vuông CE.
Vậy BC > CE.
3)Ta có: BC > BD (cmt)
BC > CE (cmt)
BC + BC > BD + CE
2BC > BD + CE
\(BC>\dfrac{BD+CE}{2}\)
1)
Xét tam giác vuông BDC, ta có:
BC là cạnh huyền
BD là cạnh góc vuông
Theo bất đẳng thức trong tam giác vuông, cạnh huyền luôn lớn hơn cạnh góc vuông.
Vậy BC > BD.
2)
Xét tam giác vuông CEB, ta có:
BC là cạnh huyền
CE là cạnh góc vuông
Theo bất đẳng thức trong tam giác vuông, cạnh huyền luôn lớn hơn cạnh góc vuông.
Vậy BC > CE.

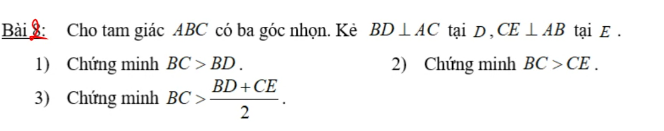




 giúp vs ạ:) e đng cần gấpppp
giúp vs ạ:) e đng cần gấpppp







