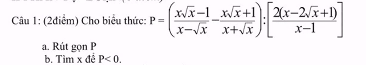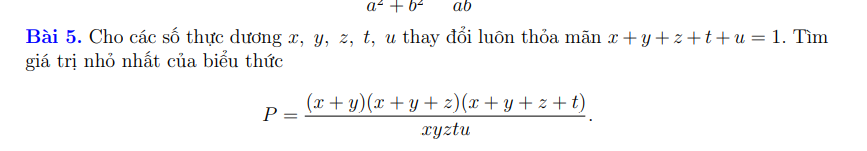Bài 3:
\(a,\) Theo tc đường kính cắt dây cung thì \(OH\bot AB;OK\bot CD\)
Ta có \(HB=KD\left(\dfrac{1}{2}AB=\dfrac{1}{2}CD\right)\)
Áp dụng PTG: \(\left\{{}\begin{matrix}OH^2=OB^2-HB^2\\OK^2=OD^2-KD^2\end{matrix}\right.\)
Mà \(OD=OB\Rightarrow OH^2=OK^2\Rightarrow OH=OK\)
\(\left\{{}\begin{matrix}OH=OK\\\widehat{OHE}=\widehat{OKE}=90^0\\OE\text{ chung}\end{matrix}\right.\Rightarrow\Delta EOH=\Delta EOK\left(ch-cgv\right)\\ \Rightarrow EH=EK\)
Lại có \(AH=HB=CK=KD\left(\dfrac{1}{2}AB=\dfrac{1}{2}CD\right)\)
Do đó \(EA=HA+HE=CK+KE=CE\left(đpcm\right)\)
Đúng 1
Bình luận (1)
